Определение значений расходов в участках гидравлической сети¶
Рассмотрим гидравлическую сеть:
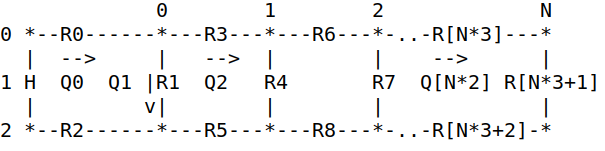
$H$, м - напор насоса, $R$ - гидравлическое сопротивление участка сети (подробнее про гидравлическое сопротивление см. в статье Моделирование характеристики гидравлической сети), $Q$, $м^3/ч$ - объёмный расход через участок сети.
Необходимо найти значения расхода в каждом участки сети при известных значениях гидравлических сопротивлений и напора насоса.
Для этого следует составить и решить систему нелинейных уравнений.
Рассмотрим сеть, состоящую из трёх потребителей. В этом случае нужно найти пять значений расходов: $Q_i,\ i = 0 \ldots 4$, для чего необходимо составить и совместно решить пять уравнений.
$$H - (R_0 + R_2)Q_0^2 - R_1Q_1^2 = 0$$$$R_1Q_1^2 - (R_3 + R_5)Q_2^2 - R_4Q_3^2 = 0$$$$R_4Q_3^2 - (R_6 + R_7 + R_8)Q_4^2 = 0$$$$Q_0 - Q_1 - Q_2 = 0$$$$Q_2 - Q_3 - Q_4 = 0$$import numpy as np #работа с массивами
N = 3 # количество потребителей
Значения гидравлических сопротивлений $R$ участков сети и значение напора насоса $H$ возьмём отсюда.
#Зададим значения гидравлических сопротивлений всех участков сети
Rs = np.array([[0.0002, 0.0002, 0.0002],
[0.0004, 0.0004, 0.0004],
[0.0005, 0.0005, 0.0005]], dtype = float)
#Напор насоса, м
H = 41.31
#Т.к. в функцию поиска корней системы нелинейных уравнений в качестве
#входного параметра передаётся одномерный массив значений первых приближений расходов,
#то все массивы придётся делать одномерными
Rs = np.reshape(Rs, N * 3, order = 'F')
Rs
#Функция, возвращающая результат вычисления входящих в систему уравнений выражений
#для переданных значений расходов Qs. Если Qs - решение системы уравнений, то
#функция возвращает массив из (2*N-1) нулей.
def func(Qs):
f = np.zeros(2 * N - 1)
#Выражение для нулевого контура - падение давления на участке R0-R1-R2 должно равняться H
f[0] = H - (Rs[0] + Rs[2]) * Qs[0] ** 2 - Rs[1] * Qs[1] ** 2
#Выражения для контуров 1 - (N-2)
for i in range(1, N-1):
j = i * 3
k = i * 2
f[i] = Rs[j-2] * Qs[k-1]**2 - (Rs[j] + Rs[j+2]) * Qs[k] ** 2 - Rs[j+1] * Qs[k+1] ** 2
#Выражения для контуров N-1
j = (N-1) * 3
k = (N-1) * 2
f[N-1] = Rs[j-2] * Qs[k-1]**2 - (Rs[j] + Rs[j+1] + Rs[j+2]) * Qs[k] ** 2
#Баланс расходов в узлах 0 - (N-2)
for i in range(N, N + N - 1):
k = (i - N) * 2
f[i] = Qs[k] - Qs[k+1] - Qs[k+2]
return f
В функцию нахождения решения системы нелинейных уравнений необходимо передавать в качестве параметра массив первых приближений значений расходов. Если значения первых приближений выбраны неудачно, то функция может не найти решение (выдать ошибку) или уйти в область отрицательных значений.
Для формирования массива первых приближений проделаем следующее. Расчитаем расход через каждый потребитель при условии отключения от подводящего и отводящего трубопроводов других потребителей кроме рассматрваемого. Затем найдём значения расходов через участки подводящего трубопровода при условии, что через каждый потребитель проходит найденный на первом этапе расход.
from math import sqrt
#Функция для определения начальных значений, передаваемых
#в функцию решения системы нелинейных уравнений в качестве первого приближения
def get_init_guess():
Qs_i = np.zeros(2*N-1)
#опрределяем расход через каждый потребитель
R_pipe = 0
for i in range(N-1):
j = i * 3
R_pipe += Rs[j] + Rs[j+2] #сопротивление подводящих и отводящих трубопроводов
R_circ = R_pipe + Rs[j+1] #суммарное сопротивление контура
Qs_i [i * 2 + 1] = sqrt(H/R_circ) #расход через контур
#Для последнего контура
j = 3 * (N-1)
k = 2 * (N-1)
Qs_i[k] = sqrt(H / (R_pipe + Rs[j] + Rs[j+1] + Rs[j+2]))
#Отределяем расход через участки подводящего трубопровода
Q = Qs_i[k]
for i in range(N-2, -1, -1):
Qs_i[2*i] = Q + Qs_i [i * 2 + 1]
Q = Qs_i[2*i]
return Qs_i
get_init_guess()
Для решения систем нелинейных уравнений применим функцию root из библиотеки scipy.optimize.
from scipy.optimize import root
#Вызываем функцию root, передав ей функцию с уравнениями и массив начальных приближений
sol = root(func, get_init_guess())
#Значения найденных расходов находится в sol.x
sol.x
#Количество выполненных приближений
sol.nfev
Проверим правильность найденных в [1] сбалансированных значений гидравлических сопротивлений линий потребителей.
Rs_b = np.array([0.008432, 0.0275, 0.0004])
for i in range(Rs_b.shape[0]):
Rs[i*3+1] = Rs_b[i]
r = root(func, get_init_guess())
r.x
Найденные значения расходов совпадают с большой степенью точности с заданными для каждого потребителя значениями расходов, значит в [1] были найдены корректные значения сбалансиованных сопротивлений линий потребителей.
N = 50 #Попробуем сделать расчёт для сети с 50 потребителями
Rs = np.random.sample(N * 3) + 1e-4 #Добавляем 1e-4 чтобы гарантированно не было нулевых сопротивлений
H = 1000 #Задаём напор насоса
sol = root(func,get_init_guess())
sol.x
#Количество выполненных приближений
sol.nfev
Проверка: выражения должны возвращать значение напора насоса
#Ближайший потребитель i = 0
(Rs[0] + Rs[2]) * sol.x[0] ** 2 + Rs[1] * sol.x[1] ** 2
#Самый дальний потребитель i = N-1
dH = 0
for i in range(N):
dH += (Rs[3*i] + Rs[3*i+2]) * sol.x[2*i] ** 2
dH + Rs[-2] * sol.x[-1] ** 2
Если в качестве значений первых пиближений для расходов принять единицы, то в ответе появятся отрицательные значения, что противоречит физическому смыслу.
root(func,np.ones(2*N-1)).x
Инженерные расчёты на Python, С.В. Медведев, 2020
Использование Python и Jupyter Notebook для инженерных расчётов, С.В. Медведев, 2020