Перекачка жидкости из двух баков в один общий бак

Рассмотрим сеть, состоящую из трёх атмосферных баков и двух насосов, предназначенных для перекачки жидкости из своего бака в общий бак.

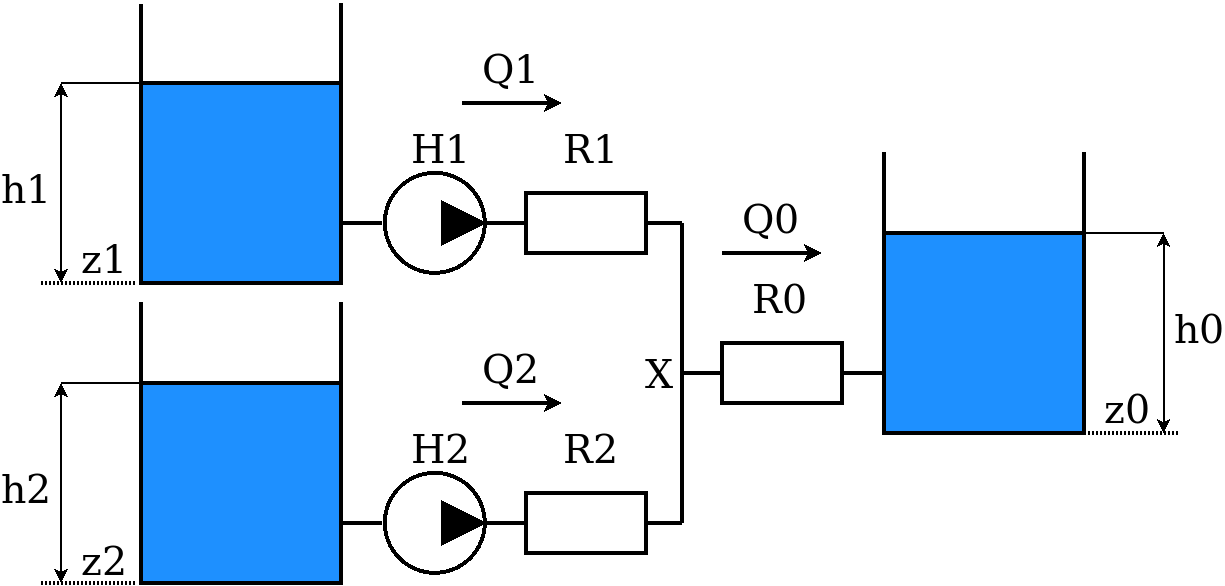
Схема

$z$ - высотная отметка основания бака (например, относительно уровня моря), м; $h$ - уровень жидкости относительно основания бака, м; $H$ - напор насоса, м; $Q$ - расход, $м^3/ч$; $R$ - гидравлическое сопротивление участка сети, X - точка соединения двух ветвей. На данном этапе примем, что напор насоса не зависит от подачи (напорная характеристика - горизонтальная линия).

Для определения расходов через участки сети необходимо решить следующую систему уравнений:

$$(z_1 + h_1) - (z_0 + h_0) + H_1 - R_1Q_1^2 - R_0Q_0^2 = 0$$$$(z_2 + h_2) - (z_0 + h_0) + H_2 - R_2Q_2^2 - R_0Q_0^2 = 0$$$$Q_0 - Q_1 - Q_2 = 0$$
In [1]:
import numpy as np
#Исходные данные
zs = np.array([1., 2., 3.]) #отметки оснований баков
hs = np.array([1., 2., 3.]) #уровни жидкости
Hs = np.array([0., 50., 45.]) #напоры насосов (у общего бака нет насоса, поэтому Hs[0] = 0)
Rs = np.array([1e-3, 1e-3, 1e-3]) #гидравлические сопротивления участков

Перед тем, как проводить расчёт, необходимо проверить систему на работоспособность (см. последний раздел данной статьи). В противном случае можно впустую потратить много времени, пытаясь добиться, чтобы из результатов расчёта исчезли отрицательные значения.

In [2]:
sols = np.zeros(3)
#Функция, возвращающая результат вычисления входящих в систему уравнений выражений
#для переданных значений расходов Qs. Если Qs - решение системы уравнений, то
#функция возвращает массив sols из трёх нулей.
def func(Qs):
    sols[0] = (zs[1] + hs[1]) - (zs[0] + hs[0]) + Hs[1] - Rs[1] * Qs[1] * Qs[1] - \
        Rs[0] * Qs[0] * Qs[0]
    sols[1] = (zs[2] + hs[2]) - (zs[0] + hs[0]) + Hs[2] - Rs[2] * Qs[2] * Qs[2] - \
        Rs[0] * Qs[0] * Qs[0]
    sols[2] = Qs[0] - Qs[1] - Qs[2]
    return sols

В функцию нахождения решения системы нелинейных уравнений необходимо передавать в качестве параметра массив первых приближений значений расходов. Если значения первых приближений выбраны неудачно, то функция может не найти решение (выдать ошибку) или уйти в область отрицательных значений.

За первое приближение примем расходы через каждую ветвь при условии отсутствия второй ветви.

In [3]:
from math import sqrt
init_guess = np.zeros(3) #первое приближение значений расходов
#Функция для определения начальных значений, передаваемых 
#в функцию решения системы нелинейных уравнений в качестве первого приближения
def get_init_guess():
    init_guess[1] = sqrt(((zs[1] + hs[1]) - (zs[0] + hs[0]) + Hs[1]) / (Rs[1] + Rs[0])) #Q1
    init_guess[2] = sqrt(((zs[2] + hs[2]) - (zs[0] + hs[0]) + Hs[2]) / (Rs[2] + Rs[0])) #Q2
    init_guess[0] = init_guess[1] + init_guess[2] #Q0
    return init_guess

Для решения системы нелинейных уравнений применим функцию root из библиотеки scipy.optimize.

In [4]:
from scipy.optimize import root
sol = root(func, get_init_guess())
#Значения найденных расходов находится в sol.x
print(*sol.x)

200.88652592951297 107.91016495227097 92.97636097706415
In [5]:
#Количество выполненных функцией root приближений
sol.nfev
Out[5]:
40

Проверка

In [6]:
#Относительная погрешность для первой линии
((Rs[1] * sol.x[1] ** 2 + Rs[0] * sol.x[0] ** 2 - ((zs[1] + hs[1]) - (zs[0] + hs[0]))) - Hs[1]) / Hs[1]
Out[6]:
1.1043255199183476e-12
In [7]:
#Относительная погрешность для второй линии
((Rs[2] * sol.x[2] ** 2 + Rs[0] * sol.x[0] ** 2 - ((zs[2] + hs[2]) - (zs[0] + hs[0]))) - Hs[2]) / Hs[2]
Out[7]:
1.2582764459997027e-11

Учёт зависимости напора насоса от подачи

Каким образом моделировать напорные характеристики насосов описано в статье Моделирование напорной характеристики насоса. Для простоты создадим функции напорных характиристик насосов, которые для любого значения подачи будут возвращать одно и тоже значение напора.

In [8]:
#Напорные характеристики насосов
def fH1 (Q):
    return Hs[1]
def fH2 (Q):
    return Hs[2]
fHs = [None, fH1, fH2]

Изменим вычисляющую выражения системы уравнений функцию, заменив Hs[i] на fHs[i](Qs[i]).

In [9]:
#Функция, возвращающая результат вычисления входящих в систему уравнений выражений
#для переданных значений расходов Qs. Если Qs - решение системы уравнений, то
#функция возвращает массив sols из трёх нулей.
def func(Qs):
    sols[0] = (zs[1] + hs[1]) - (zs[0] + hs[0]) + fHs[1](Qs[1]) - Rs[1] * Qs[1] * Qs[1] - \
        Rs[0] * Qs[0] * Qs[0]
    sols[1] = (zs[2] + hs[2]) - (zs[0] + hs[0]) + fHs[2](Qs[2]) - Rs[2] * Qs[2] * Qs[2] - \
        Rs[0] * Qs[0] * Qs[0]
    sols[2] = Qs[0] - Qs[1] - Qs[2]
    return sols
In [10]:
#Результаты расчёта должны быть теми же
sol = root(func, get_init_guess())
print(*sol.x)

200.88652592951297 107.91016495227097 92.97636097706415

Проверка системы на работоспособность

Возможна такая комбинация параметров системы, при которой один из насосов будет "заперт" насосом с большим напором. Примем, что значение напора первого насоса больше чем у второго. Определим значение напора второго насоса, при котором он перестанет прокачивать жидкость через свою линию, т.е. станет работать в режиме "на закрытую задвижку". В данном случае $Q_2 = 0; Q_{1} = Q_0$.

При $Q_{1} = Q_0$ пороговое значение $Q_{1пор}$ определяется по формуле:

$$Q_{1пор} = \sqrt{\frac{(z_1 + h_1) - (z_0 + h_0) + H_1}{R_1 + R_0}}$$

Условие "запирания" второго насоса - давление в точке X должно быть равно напору второго насоса при нулевой подаче, плюс статическое давление столба жидкости $(z_2 + h_2) - z_x$:

$$(z_2 + h_2) - z_x + H_2= (z_1 + h_1) - z_x + H_1 - R_1Q_{1пор}^2$$

Отсюда находим пороговое значение напора второго насоса:

$$H_{2пор} = (z_1 + h_1) - (z_2 + h_2) + H_1 - R_1Q_{1пор}^2$$
In [11]:
#Найдём пороговое значение напора второго насоса
Q1_marg = sqrt((zs[1] + hs[1] - (zs[0] + hs[0]) + Hs[1]) / (Rs[1] + Rs[0]))
H2_marg = zs[1] + hs[1] - (zs[2] + hs[2]) + Hs[1] - Rs[1] * Q1_marg * Q1_marg
H2_marg
Out[11]:
22.0
In [12]:
Hs[2] = H2_marg #Hs[2] используется при нахождении первого приближения
#изменяем функцию напорной характеристики второго насоса
def fH2_m (Q): 
    return H2_marg
fHs[2] = fH2_m
In [13]:
#Q2 должно быть близким к нулю
sol = root(func, get_init_guess())
print(*sol.x)

161.24515496596516 161.24515496598903 -2.4555529072868164e-11

Ссылки

  1. Моделирование характеристики гидравлической сети
  2. Моделирование напорной характеристики насоса

Инженерные расчёты на Python, С.В. Медведев, 2020
Использование Python и Jupyter Notebook для инженерных расчётов, С.В. Медведев, 2020