Поверочный расчёт теплообменника

В данной статье описана методика проведения поверочного расчёта теплообменника прямоточного и противоточного типа и пример выполнения поверочного расчёта с использованием класса HeatExchanger из модуля heatexchanger (скачать).

Отвод

По результатам конструкторского расчёта известны проектные значения следующих параметров теплообменника:

$t_х^{вх}$ - температура холодного потока на входе в теплообменник, C;
$t_х^{вых}$ - температура холодного потока на выходе из теплообменника, C;
$t_г^{вх}$ - температура горячего потока на входе в теплообменник, C;
$t_г^{вых}$ - температура горячего потока на выходе из теплообменника, C;
$Q_х$ - тепловая мощность, получаемая холодным потоком от горячего, Вт;
$C_х$ - теплоёмкость холодного потока, Дж/(кг⋅с);
$C_г$ - теплоёмкость горячего потока, Дж/(кг⋅с);
$F$ - площадь поверхностей теплообмена, $м^2$;
$k$ - коэффициент теплопередачи, $Вт/(м^2\cdot K)$,
$\eta$ - КПД теплообменника.

$$Q_х = k \overline{\Delta t} F\qquad \qquad (1)$$

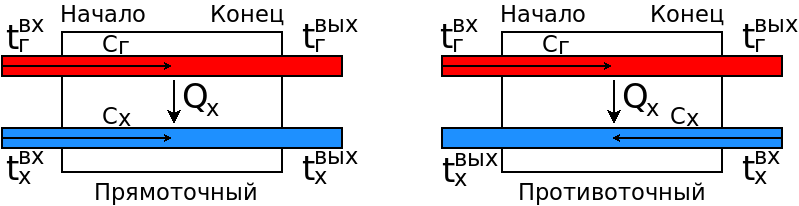
где $\overline{\Delta t}$ - среднее значение температурного напора $$\overline{\Delta t} = \frac{\Delta t_{нач} - \Delta t_{кон}}{\ln(\Delta t_{нач}/\Delta t_{кон})}$$ Для теплообменника прямоточного типа $$\Delta t_{нач} = t_г^{вх} - t_{х}^{вх};\, \Delta t_{кон} = t_г^{вых} - t_{х}^{вых}$$ Для теплообменника противоточного типа $$\Delta t_{нач} = t_г^{вх} - t_{х}^{вых};\, \Delta t_{кон} = t_г^{вых} - t_{х}^{вх}$$

Для того чтобы нагревать в теплообменнике поток холодной жидкости с массовым расходом $G$ (кг/с) теплоёмкостью $c_p$ (Дж/(кг$\cdot$К)) на $\Delta t$ градусов, необходимо подводить к рассматриваемому потоку тепловую мощность $Q_х$, Вт. При этом горячий поток жидкости отдаёт тепловую мощность $Q_г = Q_х/\eta$, где $\eta$ - КПД теплообменника.

$$Q = Gc_p\Delta t$$

или $$Q = С\Delta t$$ где $C = Gc_p$ - теплоёмкость потока, Дж/(кг$\cdot$с)

$$Q_х = C_{х}(t_{х}^{вых} - t_х^{вх})\qquad \qquad (2)$$$$Q_х = C_{г}(t_г^{вх} - t_{г}^{вых})\eta\qquad \qquad (3)$$

$C_{х}$, $C_{г}$ - теплоёмкость холодного и горячего потока соответственно. Т.к. теплоёмкости рабочих сред холодного и горячего потоков можно считать неизменными, то изменение теплоёмкости потока будет однозначно определяться изменением массового расхода рабочей среды.

Итак, в нашем распоряжении имеются три уравнения и семь независимых параметров: $t_х^{вх}$, $t_х^{вых}$, $t_г^{вх}$, $t_г^{вых}$, $C_{х}$, $C_{г}$, $Q_х$.

Учёт изменения значения коэффициента теплопередачи при изменении расхода рабочей среды¶

При изменении скорости течения рабочей среды (величины расхода) внутри теплообменника коэффициент теплопередачи теплообменника изменяется.
Без учёта термического сопротивления стенки, разделяющей два потока, формула для вычисления коэффициента теплопередачи имеет вид:

$$k = \frac{1}{1/\alpha_г + 1/\alpha_х} = \frac{\alpha_г \alpha_х}{\alpha_г + \alpha_х}$$

где $\alpha_г$, $\alpha_х$ - коэффициент теплоотдачи от горячего и к холодному потоку соответственно. Т.к. нам неизвестно как соотносятся между собой значения коэффициентов теплоотдачи горячего и холодного потоков, примем, что они равны.

$$k = \frac{\alpha \alpha}{\alpha + \alpha} = \frac{\alpha}{2}$$

Согласно формуле М. А. Михеева коэффициент теплопередачи при числе Рейнольдса $Re \ge 10^4$ (турбулентный режим течения) пропорционален $Re^{0.8}$. Коэффициент Рейнольдса $Re$ пропорционален скорости, а значит расходу потока, который в свою очередь, пропорционален теплоёмкости потока $C$.

Коэффициент теплопередачи при расходах отличных от проектных значений равен:

$$k = \frac{2k_п(ab)^{0.8}}{a^{0.8} + b^{0.8}}$$

где $k_п$ - проектное значение коэффиента теплопередачи, $a = C_г/C_г^п$, $b = C_х/C_х^п$, где $C$ - теплоёмкость потока в рассматриваемом режиме работы, $C^п$ - проектное значение теплоёмкости потока.

Пример поверочного расчёта теплообменника¶

Рассмотрим пластинчатый маслоохладитель (противоточный) со следующими проектными параметрами:

$Q_х = 450\, кВт$
$t_{г}^{вх} = 70\,^{\circ}C$
$t_{г}^{вых} = 55.3\,^{\circ}C$
$t_{х}^{вх} = 52\,^{\circ}C$
$t_{х}^{вых} = 56\,^{\circ}C$
$\eta = 0.97$

Рассмотрим случай при котором $t_{х}^{вх} = 45\,^{\circ}C$, параметры маслоохладителя на стороне масла должны остаться неизменными. Следует найти $С_х$, $t_{х}^{вых}$, для этого данным параметрам следует присвоить None.

Предположим, мы хотим, чтобы при неизменной тепловой мощности маслоохладителя охлаждающая вода нагревалась в маслоохладителе на 6.5 градусов.

Если количество искомых параметров задано больше необходимого для нахождения единственного возможного решения, то будет выдано первое найденное (из бесконечного множества) решение.

Если количество искомых параметров задано меньше необходимого (введены избыточные ограничения), то будет выдана ошибка.

In [10]:

params = he.get_inp_params()
params['t_cold_in'] = 45; params['t_cold_out'] = params['t_cold_in'] + 6.5; params['C_cold'] = None
params['t_hot_in'] = None; #params['t_hot_out'] = None
he.calc(params)
he.get_res()

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-10-66d168af7968> in <module>
      2 params['t_cold_in'] = 45; params['t_cold_out'] = params['t_cold_in'] + 6.5; params['C_cold'] = None
      3 params['t_hot_in'] = None; #params['t_hot_out'] = None
----> 4 he.calc(params)
      5 he.get_res()

~/dzen/0025_Теплообменник/heatexchanger.py in calc(self, params)
    130             return self.res
    131         else:
--> 132             raise ValueError("Решение не найдено. Скорее всего задано слишком мало искомых параметров.")
    133 
    134     def get_inp_params(self, des=True):

ValueError: Решение не найдено. Скорее всего задано слишком мало искомых параметров.

Поверочный расчёт теплообменника¶

Учёт изменения значения коэффициента теплопередачи при изменении расхода рабочей среды¶

Пример поверочного расчёта теплообменника¶