[Статьи]

Расчёт кавитационного запаса насоса

Кавита́ция (от лат. cavitas — пустота) — физический процесс образования пузырьков (пустот) в жидких средах, с последующим их схлопыванием и высвобождением большого количества энергии, которое сопровождается шумом и гидравлическими ударами.

В насосах кавитация возникает в результате местного понижения давления жидкости до давления кипения при температуре жидкости, в результате чего часть жидкости переходит из жидкой фазы в газообразную, и в потоке жидкости образуются пузырьки газа. Попадая в зону с более высоким давлением (выше давления кипения при текущей температуре), пузырьки газа схлопываются (газ конденсируется).

Давление с одной стороны может абсолютным и избыточным, с другой - полным, статическим и динамическим.
Абсолютное давление – это давление относительно вакуума, оно измеряется барометром. Нормальное атмосферное давление 101325 Па – это абсолютное давление.
Избыточное давление – это разница между измеряемым абсолютным давлением и атмосферным давлением, измеряется манометром. В данной статье используются абсолютные величины давления.
Полное, статическое и динамическое давления связаны зависимостью:

$$\bar{p} = p + \frac{\rho w^2}{2}\quad (1)$$

где $\bar{p}$ - полное давление, Па; $p$ - статическое давление, Па; $\rho w^2/2$ -динамическое давление, Па; $\rho$ - плотность жидкости, $кг/м^3$; $w$ - скорость жидкости, м/с.

Надкавитационный напор (кавитационный запас) обычно задаётся в метрах столба жидкости (м). Перевод давления из Па в метры столба жидкости (м): $$H = \frac{p}{\rho g} $$ где $H$ - давление в метрах столба жидкости; $p$ - давление в Па; $\rho$ - плотность жидкости, $кг/м^3$; $g\approx$9,81 $м/с^2$ - ускорение свободного падения.

В метрах столба жидкости (м) выражение (1) выглядет следующим образом:

$$\bar{H} = H + \frac{w^2}{2g}\quad$$

где $\bar{H}$ - полное давление, м; $H$ - статическое давление, м; $ w^2/(2g)$ -динамическое давление, м. Когда мы говорим о давлении, при котором закипает жидкость, имеется в виду статическое давление.

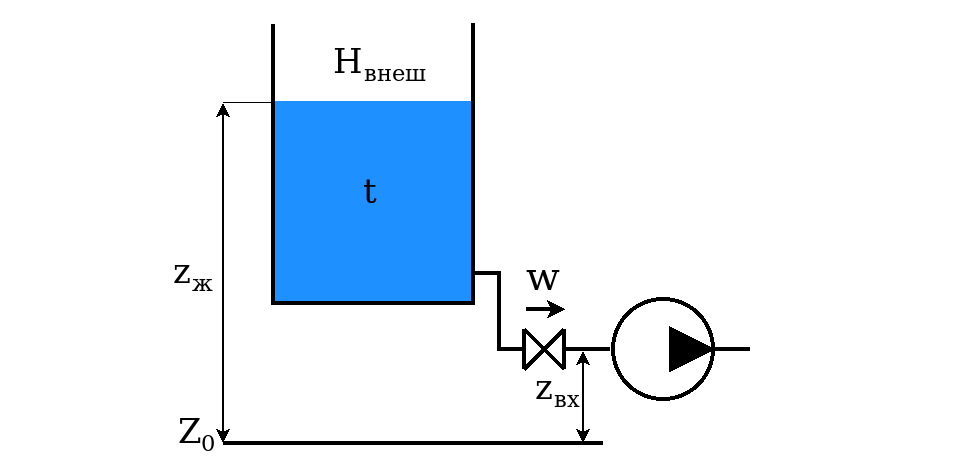
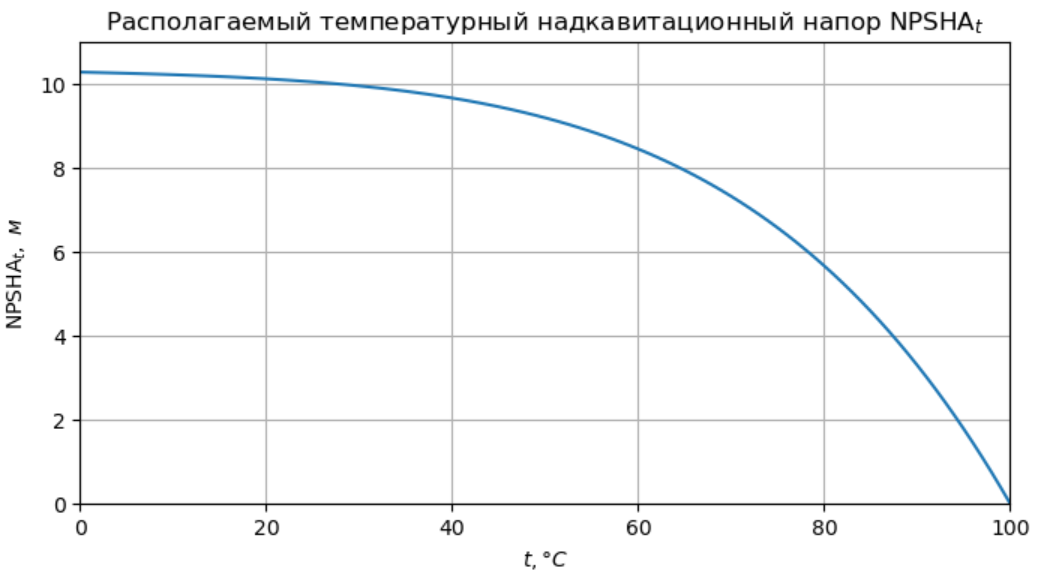
Надкавитационный напор на входе (кавитационный запас), NPSH (net positive suction head) - полное абсолютное давление жидкости в сечении входного патрубка насоса за вычетом давления кипения жидкости при данной температуре жидкости.

Располагаемый (available) надкавитационный напор NPSHA находится по формуле:

$$\mathrm{NPSHA} = \bar{H}_{вх} - H_{кип} \quad (2)$$

где $\bar{H}_{вх}$ - полное абсолютное давление жидкости в сечении фланца всасывающего патрубка насоса (на входе в насос), $H_{кип}$ - давление кипения жидкости (м) при температуре равной температуре жидкости $t$.

Развернув $\bar{H}_{вх}$, получим следующее выражение:

$$\mathrm{NPSHA} = H_{внеш} + (z_ж - z_{вх}) - \Delta H + \frac{w^2}{2g} - H_{кип} \quad (3)$$

где $H_{внеш}$ - давление над поверхностью жидкости в исходном баке (для открытой системы - атмосферное давление $H_{атм}$), м; $(z_ж - z_{вх})$ - давление (подпор) столба жидкости, м; $z_ж$ - отметка поверхности жидкости относительно произвольно выбранной плоскости отсчёта $Z_0$, м; $z_{вх}$ - отметка оси входного патрубка, м; $\Delta H$ - потери давления (напора) при движении жидкости объёмным расходом $Q$ ($м^3/ч$) в подводящем трубопроводе, м.

Одной из основных характеристик насоса является требуемый (required) надкавитационный напор $\mathrm{NPSHR}$. Если $\mathrm{NPSHR} = 5$ м, то это не значит, что для недопущения кавитации перед насосом нужно создать подпор не менее 5 м.

Условие бескавитационной работы насоса: $\mathrm{NPSHR} < (\mathrm{NPSHA} - 0.5\ м)$, где $0.5\ м$ - запас.

Из выражения (2) следует, что при прочих равных условиях чем ниже $H_{кип}$ (зависящая от температуры жидкости $t$), тем выше $\mathrm{NPSHA}$.

Запишем выражение (3) в следующем виде:

$$\mathrm{NPSHA} = \mathrm{NPSHA}_t + (z_ж - z_{вх}) - \Delta H + \frac{w^2}{2g} \quad (4)$$

где $\mathrm{NPSHA}_t = H_{внеш}-H_{кип}$ - располагаемый температурный надкавитационным напор, разность между внешним давлением и давлением, при котором закипает жидкость температурой $t$.

Для открытой системы внешним давлением является атмосферное давление ($H_{внеш}=H_{атм}$) и зависимость $\mathrm{NPSHA}_t$ от температуры воды выглядит следующим образом.

Из данного графика видно, что при $\mathrm{NPSHR} = 5$ м и температуре воды $20\ ^{\circ} C$ насос не только не требует подпора, но он будет работать без кавитации при заборе воды с уровня не ниже 5 м от оси всаса насоса (потери давления в подводящем трубопроводе не учитываются $\Delta H = 0$ м).

$\mathrm{NPSHR}$ зависит от расхода через насос (подачи насоса). При неизменной величине полного давления перед насосом увеличение расхода означает увеличение скорости потока, а значит уменьшения статического давления.

$$H = \bar{H} - \frac{w^2}{2g}\quad$$

Кавитация возникает при снижении статического давления в потоке до давления кипения при температуре равной температуре воды. При увеличении подачи и уменьшении статического давления снижается температура кипения воды, т.е. вода закипает при более низкой температуре, поэтому для недопущения кавитации при увеличении подачи $\mathrm{NPSHR}$ так же должен увеличиваться.

Также нужно помнить, что потери давления в трубопроводе пропорциональны квадрату скорости жидкости в нём, поэтому при увеличении подачи насоса в 2 раза потери полного давления в подводящем трубопроводе увеличатся в 4 раза.

Пример расчёта кавитационного запаса

При расчёте кавитационного запаса используются следующие ранее разработанные инструменты:

1. Определение плотности воды по температуре и давлению (см. [1]);
2. Определение давления насыщенного водяного пара (давление кипения воды) по температуре [2];
3. Определение значения динамической вязкости воды по температуре и плотности [3];
4. Расчёт потерь давления при движении жидкости в трубопроводе [4].

Все необходимые для расчёта кавитационного запаса модули на Python собраны в один архив (скачать).

Разработана методика оценки располагаемого кавитационного запаса без необходимости проведения сложных расчётов (см. [5]).

from npsh import calc_NPSH  # расчёт имеющегося надкавитационного напора на входе в насос
from region1 import Region1  # расчёт параметров воды
from calcwsdvisc import calc_ws_dvisc  # расчёт динамической вязкости воды
from hydrcalc import ppln_calc_dH, ppln_get_defs  # расчёт потерь давления в трубопроводе

Исходные данные

Необходимо рассмотреть самое неблагоприятное для обеспечения безкавитационной работы насоса сочетание внешних условий. Подводящий трубопровод 89х3,5, внутренний диаметр входного патрубка насоса 40 мм, расход воды 10 $м^3/ч$, шероховатость внутренних стенок 0,3 мм.

p = 101325 * 0.95  # давление над поверхностью воды (предельно низкое атмосферное давление), Па
t = 90  # температура воды, С
z_s = .6  # высотная отметка поверхности воды в баке (минимальный уровень), м
z_p = -1.33  # высотная отметка оси входного патрубка насоса, м
Q = 10.  # объёмный расход, м3/ч
D = 0.082  # внутренний диаметр подводящего трубопровода, м
D_p = 0.04  # внутренний диаметр входного патрубка насоса, м

r1 = Region1()
dens = 1 / r1.props_tp(t,p)['v']  # плотность воды, кг/м3 (см. [1])
dens

965.316345049121

dvisc = calc_ws_dvisc(t, dens)  # динамическая вязкость воды, Па*с (см. [3])
kvisc = dvisc / dens  # кинематическая вязкость воды, м2/с
kvisc  # кинематическая вязкость потребуется при расчёте потерь давления в подводящем трубопроводе

3.254676957062171e-07

Расчёт потерь давления в подводящем трубопроводе

Подробно методика расчёта потерь давления в подводящем трубопроводе описана в [4].

defs = ppln_get_defs(0.082)  # труба 89х3,5
defs

{'D': 0.082, 'Delta': 0.0002, 'kvisc': 1e-06, 'deg': 90, 'RD': 1.5, 'qty': 1}

defs['Delta'] = 0.3e-3; defs['kvisc'] = kvisc

enter = {'type': 'lrc', 'value': 0.5} # вход в трубопровод
pipe = {'type': 'pipe', 'qty': 6}  # труба DN80
elbow = {'type': 'elbow', 'qty': 4}  # отвод 90 градусов
elbow45 = {'type': 'elbow', 'deg': 45, 'qty': 2}  # отвод 45 градусов
valve = {'type': 'lrc', 'value': 0.05} # задвижка фланцевая
pipe40 = {'type': 'pipe', 'D': D_p, 'qty': 0.25}  # труба DN40
exit = {'type': 'lrc', 'value': 1, 'D': D_p} #потери с выходной скоростью
elems = [enter, pipe, elbow, elbow45, valve, pipe40, exit]
dHs = ppln_calc_dH(Q, elems, **defs)
dHs  # потери давления на каждом участке

[0.007053085674501933,
 0.02948566819409823,
 0.0263979868482122,
 0.007729500539364892,
 0.0007053085674501934,
 0.0540900501356391,
 0.24912918035832818]

dH = sum(dHs)  # суммарное значение потерь давления, м
dH

0.37459078031759474

Расчёт кавитационного запаса

help(calc_NPSH)  # описание функции calc_NPSH

Help on function calc_NPSH in module npsh:

calc_NPSH(z_s, z_p, t, p=101325, Q=0, D=0, dH=0)
    Расчёт имеющегося надкавитационного напора NPSHA (кавитационного запаса)
    z_s: высотная отметка поверхности воды, м
    z_p: высотная отметка оси входного патрубка насоса, м
    t: температура воды, С
    p: давление над поверхностью воды, Па. По умолчанию 101325 Па.
    Q: объёмный расход, м3/ч. По умолчанию 0 
    (при расчёте NPSH скорость потока не учитывается)
    D: внутренний диаметр входного патрубка насоса, м. По умолчанию 0
    (при расчёте NPSH скорость потока не учитывается)
    dH: потери давления во входном трубопроводе насоса, м. По умолчанию 0
    (при расчёте NPSH потери давления не учитывается)
    return: значение NPSH, м

NPSHA = calc_NPSH(z_s, z_p, t, p, Q, D_p, dH)  # расчёт кавитационного запаса, м
NPSHA

4.559129372819385

Требуемый надкавитационный напор на входе $\mathrm{NPSHR}$ (required $\mathrm{NPSH}$) должен быть на 0,5 м меньше найденного значения $\mathrm{NPSHA}$:

NPSHR = NPSHA - 0.5
NPSHR

4.059129372819385

Если потери на выходе из трубопровода принимаются как $w^2/(2g)$ то их можно в $\Delta H$ не включать, и для нахождения $\mathrm{NPSHA}$ использовать упрощённую формулу (3):

$$\mathrm{NPSHA} = H_{внеш} + (z_ж - z_{вх}) - \Delta H' - H_{кип}$$

где $\Delta H' = \Delta H - w^2/(2g)$.

В этом случае в функцию calc_NPSH передавать параметры Q и D не нужно.

# Вычисления NPSHR при не включении в потери давления в трубопроводе
# потерь на выходе из трубопровода 
NPSHR = calc_NPSH(z_s, z_p, t, p, dH = sum(dHs[:-1])) - 0.5
NPSHR

4.0591293728193865

Ссылки

1. Расчёт теплофизических свойств воды и водяного пара. Область 1 - вода.
2. Зависимость температуры насыщения водяного пара от давления и зависимость давления насыщения от температуры
3. Определение динамической вязкости воды и водяного пара
4. Гидравлический расчёт трубопровода
5. Способ быстрой оценки кавитационного запаса насоса
6. ГОСТ ISO 9906-2015 Насосы динамические. Гидравлические испытания. Классы точности 1, 2 и 3.

Инженерные расчёты на Python, С.В. Медведев, 2020-2024
Использование Python и Jupyter Notebook для инженерных расчётов, С.В. Медведев, 2020-2024