Гидравлический разделитель (гидрострелка)¶
Здесь приведена расчётная часть статьи о гидравлическом разделителе. Расчёты выполнены для схемы без гидравлического разделителя.
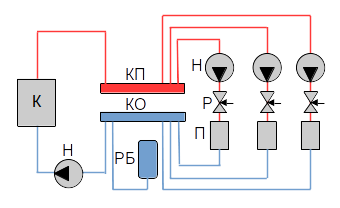
К - котёл, Н - насос, КП - коллектор прямой воды (горячая), КО - коллектор обратной воды (холодная), РБ - расширительный бак, Р - регулятор, П - потребитель тепловой энергии.
Так как гидравлический разделитель разделяет систему на изолирование участки, то для схемы с гидравлическим разделителем расчёт параметров каждого изолированного участка сводится к применению формулы (более подробно см. [1]):
$$\Delta p = RQ^2,$$где $\Delta p$ - ротери давления теплоносителя на границах участка; $R$ гидравлическое сопротивление участка; $Q$ - расход теплоносителя через участок.