Оценка величины экономии электроэнергии при использовании частотно-регулируемого привода (ЧРП) насоса¶
Из Википедии:
Частотно-регулируемый привод (частотно-управляемый привод, ЧУП, Variable Frequency Drive, VFD) — система управления частотой вращения ротора асинхронного (или синхронного) электродвигателя. Состоит из собственно электродвигателя и частотного преобразователя.
Рассмотрим систему теплоснабжения с одним потребителем тепла.
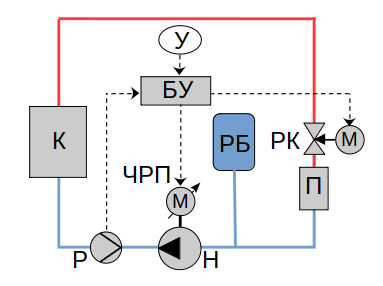
Рис. 1
К - водогрейный котёл, Н - насос с ЧРП, М - электропривод, Р - расходомер, РБ - расширительный бак, РК - регулирующий клапан с электроприводом, П - потребитель тепла, БУ - блок управления, У - уставка по расходу. Красным цветом обозначены трубопроводы прямой сетевой воды (горячая вода), синим - обратной сетевой воды (холодная вода).
Давление на всасе насоса задаётся давлением в расширительном баке. В нашем случае абсолютные значения давления в различных точках системы не имеют значения. Для нас важно то, что для каждого режима работы (величины расхода теплоносителя) потери давления в системе равны напору насоса.
Расход в системе зависит как от параметров насоса, так и от свойств гидравлической сети. Расход можно регулировать изменяя гидравлическое сопротивление сети или изменяя частоту вращения вала насоса. Гидравлическое сопротивление сети изменяется путём изменения гидравлического сопротивления регулирующего клапана. При уменьшении площади проходного сечения РК (при прикрытии) его гидравлическое сопротивление увеличивается, и наоборот, при увеличении площади проходного сечения РК (при открытии) - гидравлическое сопротивление уменьшается.
Гидравлическое сопротивление находится по формуле $R = \Delta H/ Q^2$, где $\Delta H$ - потери давления (напора); $Q$ - расход при котором имеют место потери давления $\Delta H$. Характеристика гидравлической сети - парабола (см. [1]).
Частота вращения вала насоса регулируется посредством изменения частоты переменного тока в обмотке статора электродвигателя. Примем, что на выходе частотного преобразователя (далее - ЧП) частота переменного тока может изменяться в диапазоне от 25 Гц до 50 Гц. Если для привода насоса используется асинхронный электродвигатель, то частота вращения вала насоса будет ниже частоты переменного тока на выходе ЧП. Будем считать, что при изменении частоты тока на $n$% частота вращения вала насоса так же изменится на $n$%.
Изменение подачи насоса прямо пропорционально изменению частоты вращения его вала, напора насоса - квадрату изменения частоты вращения вала (см. [2]).
Если частота переменного тока на выходе ЧП составляет 25 Гц, то величина подачи насоса составляет 50% от величины подачи при частоте 50 Гц (0,5 = 25 /50 ), а напор - 25% от напора при 50 Гц (0,25 = 0,5^2).