Рис. 1
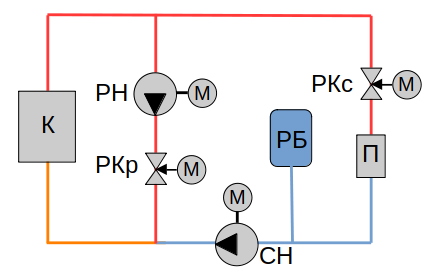
К - водогрейный котёл, П - потребитель тепловой энергии, СН - сетевой насос, РН - рециркуляционный насос, РКс - регулирующий клапан в линии сетевого насоса, РКр - регулирующий клапан в линии рециркуляции, РБ - расширительный бак, М - электропривод, синий цвет - обратная сетевая вода (остывшая), красный - прямая сетевая вода (горячая), оранжевый - вода на входе в котёл (смесь обратной и прямой сетевой воды).
Для недопущения возникновения низкотемпературной коррозии элементов котла необходимо, чтобы температура поверхностей теплообмена со стороны продуктов сгорания была выше температуры конденсации содержащегося в продуктах сгорания водяного пара (см. [1]).
Насос рециркуляции предназначен для поддержании температуры воды на входе в котёл (или котёл-утилизатор) не менее заданного значения путём подачи нагретой в котле воды на его вход.
Требуемую подачу насоса рециркуляции можно найти по упрощённой формуле (в точной формуле вместо температур используются энтальпии): $$Q_р = Q_с \frac{t_ц - t_о}{t_п - t_ц}$$ где $Q_р,\ Q_с$ - расход в линии рециркуляции и в линии сетевого насоса (потребителя) соответственно, $t_ц$, $t_о$, $t_п$ - целевое значение теплоносителя на входе в котёл, температура обратной сетевой воды, температура прямой сетевой воды соответственно.
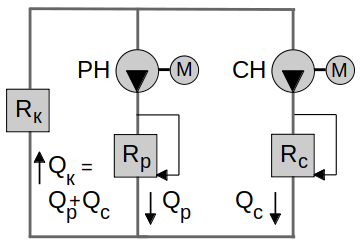
Расход через котёл составит $Q_к = Q_с + Q_р$
Расход через потребителя поддерживается постоянным с помощью РКс, тепловая нагрузка регулируется изменением температуры прямой сетевой воды (качественный метод регулирования). Расход в линии рециркуляции регулируется изменением сопротивления РКр.
Примем, что расход через потребителя (подача сетевого насоса) постоянен, составляет $Q_с=100\ м^3/ч$, и при данном расходе потери давления в ветке котла равны $dH_к=5$ м, а на потребителе $dH_п=40$ м.