Моделирование процесса расширения пара в паровой турбине¶

Для создания модели парогазовой установки (ПГУ) необходимо иметь в наличии модель котла-утилизатора (КУ) и модель паровой турбины (ПТ). Для ГТУ модель не нужна - достаточно знать её мощность, а также температуру и массовый расход выхлопных газов. У нас есть модель котла-утилизатора одного давления (см. [1]) на основании которой будет в дальнейшем разработана модель котла-утилизатора двух давлений.

В данной статье мы создадим модель паровой турбины.

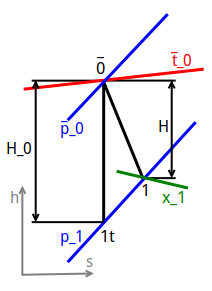Пар температурой $\bar{t}_0$ и давлением $\bar{p}_0$ (параметры торможения) поступает на вход в паровую турбину, в процессе своего расширения совершает удельную работу $H$ и выходит из паровой турбины при давлении $p_1$.

Разница в величинах между располагаемым теплоперепадом $H_0$ и использованным теплоперепадом $H$ определяется внутренним КПД проточной части паровой турбины $\eta_{0i}$: $H = \eta_{0i}H_0$.

Пара значений $\bar{t}_0$, $\bar{p}_0$ при заданном значении $\eta_{0i}$ должна быть подобрана таким образом, чтобы в точке 1 степень сухости пара была не ниже заданного значения (например 87%). Чем ниже степень сухости (чем выше степень влажности) пара тем большее количество капель выделяется в последних ступенях турбины, которые вызывают механический износ (эрозию) рабочих лопаток и снижение КПД турбины.

Строго говоря, при определении степени сухости пара за ПТ $\eta_{0i}$ не должен учитывать потери с выходной скоростью, т.к. учёт данных потерь уменьшает КПД и завышает степень сухости, но мы данный нюанс принимать в расчёт не будем.

Создадим класс ST (steam turbine - паровая турбина) в который кроме функции расчёта параметров пара на входе и выходе ПТ включим методы, позволяющие находить для пара на входе в ПТ давление при заданной температуре и температуру при заданном давлении при которых степень сухости пара на выходе из ПТ будет равна заданному значению.

В классе используется модуль wsprops, позволяющий определять теплофизические свойства воды и водяного пара (см. [2]).

In [1]:
from scipy.optimize import root_scalar
from wsprops import HSDiag  # см. [2]
"""
Модель паровой турбины
"""
class ST:
    def __init__(self, t_0, p_0, p_1 = 4500, КПД = 0.85):
        self.t_0 = t_0  # температура торможения пара на входе в ПТ, С
        self.p_0 = p_0  # давление торможения пара на входе в ПТ, Па
        self.p_1 = p_1  # статическое давление пара на выходе ПТ, Па
        self.КПД = КПД  # внутренний КПД проточной части ПТ
        self.H_0 = None  # располагаемый теплоперепад ПТ, Дж/кг
        self.H = None  # использованный теплоперепад ПТ, Дж/кг
        self.props_0 = None  # значения параметров пара на входе в ПТ
        self.props_1t = None  # значения параметров пара на выходе ПТУ при КПД=100%
        self.props_1 = None  # значения параметров пара на выходе ПТУ при заданном КПД
        self.x_1 = None  # степень сухости пара на выходе ПТ
        self.hs = HSDiag()  # объект класса "hs-диаграмма"
    def calc(self):
        """
        Расчёт параметров пара на входе и выходе паровой турбины.
        """
        self.props_0 = self.hs.props_tp(self.t_0, self.p_0)
        h_0 = self.props_0['h']
        s_1_t = self.props_0['s']
        h_1_t = self.hs.props_ps(self.p_1, s_1_t)['h']
        self.props_1t = self.hs.props_ph(self.p_1, h_1_t)
        self.H_0 = h_0 - h_1_t  # теоретический теплоперепад
        self.H = self.H_0 * self.КПД  # реальный теплоперепад
        h_1 = h_0 - self.H
        self.props_1 = self.hs.props_ph(self.p_1, h_1)
        self.x_1 = self.props_1['x']
        
    def find_p_for_x(self, x, ps = [1e5, 30e6]):
        """
        Подбор давления для заданной температуры, при котором степень сухости
        пара за ПТУ будет равна заданному x
        x: целевое значение степени сухости пара за ПТУ, доли
        st: объект класса ST (паровая турбина)
        ps: границы диапазона поиска решения (нужен для root_scalar)
        return: искомое значение давления, Па
        """
        def f(p):
            self.p_0 = p
            self.calc()
            return self.x_1 - x
        sol = root_scalar(f, bracket = ps)
        return sol.root
    
    def find_t_for_x(self, x, ts = [150, 650]):
        """
        Подбор температуры для заданного давления, при котором степень сухости
        пара за ПТУ будет равна заданному x
        x: целевое значение степени сухости пара за ПТУ, доли
        st: объект класса ST (паровая турбина)
        ps: границы диапазона поиска решения (нужен для root_scalar)
        return: искомое значение температуры, C
        """
        def f(t):
            self.t_0 = t
            self.calc()
            return self.x_1 - x
        sol = root_scalar(f, bracket = ts)
        return sol.root

В парогазовых установках с котлом утилизатором двух давлений пар вырабатывается в двух контурах - контуре высокого давления и в контуре низкого давления. Найдём для различных значений внутреннего КПД паровой турбины параметры пара $\bar{t}_0$ и $\bar{p}_0$ на входе в паровую турбину при которых степень сухости пара на выходе из турбины будет равна 87% (степень влажности 13%). Будем считать, что пар из каждого контура поступает в собственную турбину.

In [2]:
import numpy as np
p_к = 4500  # давление в конденсаторе ПТ, Па
x_к = 0.87  # целевая степень сухости пара за последней ступенью ПТ
hs = HSDiag()  # см. [2]
ts_вд = np.linspace(450, 580)  # диапазон температур пара в контуре ВД
КПДы = np.array([0.75, 0.8, 0.85, 0.9, 1]) # КПД ПТ
st = ST(None, None, p_к)  # создаём экземпляр объекта ST
def f(t, КПД):
    st.t_0 = t
    st.КПД = КПД
    return st.find_p_for_x(0.87, [1e5, hs.region2.bound23.p_T(t+273.15)-1])
ps_вд = np.array([[f(t, КПД) for КПД in КПДы] for t in ts_вд])
In [3]:
ts_нд = np.linspace(150, 300)  # диапазон температур пара в контуре НД
ps_нд = np.array([[f(t, КПД) for КПД in КПДы] for t in ts_нд])
In [4]:
ts = [ts_вд, ts_нд]; ps = [ps_вд, ps_нд]
import matplotlib.pyplot as plt
fig, axes = plt.subplots(2, 1, figsize = (8, 8))
fig.suptitle(f"Степень сухости пара за ПТ {int(x_к * 100)}%, $p_к=${round(p_к/1000, 1)} кПа", y = 0.92)
for i, ax in enumerate(axes):
    ax.set_ylabel('$p_0,\ МПа$');
    ax.set_xlabel('$t_0, \degree C$'); ax.plot(ts[i], ps[i]/1e6, label = np.intc(КПДы * 100)); ax.grid();
    ax.legend(title = 'КПД ПТ, %');
axes[0].set_xlim(460, 580); axes[0].set_ylim(0., 30);
axes[1].set_xlim(160, 300); axes[1].set_ylim(0., 3);

Верхний график относится к контуру высокого давления, нижний - к контуру низкого давления. Увеличение давления при неизменной температуре уменьшает степень сухости пара на выходе ПТ, увеличение температуры при неизменном давлении увеличивает степень сухости пара.

Посмотрим как соотносятся друг с другом мощности турбин контура высокого и контура низкого давлений. Согласно данным с сайта Интер РАО - Инжиниринг на Ивановских ПГУ установлен котёл утилизатор Е-148/35-6.7/0.6-493/229 откуда следует, что $D^{вд}$ = 148 т/ч, $D^{нд}$ = 35 т/ч, $p_0^{вд}$ = 6,7 МПа, $t_0^{вд}$ = 493 $^\circ C$, $p_0^{нд}$ = 0,6 МПа, $t_0^{нд}$ = 229 $^\circ C$.

In [5]:
D_вд = 148 / 3.6; D_нд = 35 / 3.6  # расход пара в контуре ВД и НД, кг/с
p_0_вд = 6.7e6; p_0_нд = 0.6e6  # давление пара в контуре ВД и НД, Па
t_0_вд = 493; t_0_нд = 229  # температура пара в контуре ВД и НД, C
# Создадим экземпляры класса ST для ПТ ВД и ПТ НД
st_вд = ST(t_0_вд, p_0_вд, p_к); st_вд.calc()
st_нд = ST(t_0_нд, p_0_нд, p_к); st_нд.calc()
N_вд = st_вд.H * D_вд / 1e6; N_нд = st_нд.H * D_нд / 1e6
N_вд, N_нд, N_нд / N_вд * 100
# МВт, МВт, %
Out[5]:
(46.6944258952966, 6.295421814951322, 13.482169861275544)

Проверим степень сухости пара за ПТ

In [6]:
st_вд.x_1, st_нд.x_1,
Out[6]:
(0.878327704667592, 0.8798325948631802)

Мощность, вырабатываемая паром контура низкого давления составляет 13,5% от мощности, вырабатываемой паром контура высокого давления.

In [7]:
N_гту = 110 # Мощность ГТУ на Ивановских ПГУ
N_пгу_вд = N_гту + N_вд  # мощность ПГУ без контура низкого давления
N_нд / N_пгу_вд  # относительное увеличение мощности ПГУ при добавлении контура НД
Out[7]:
0.040176424776960026
In [8]:
КПД_гту = 0.35  # КПД ГТУ на Ивановских ПГУ
N_топл = N_гту / КПД_гту  # тепловая мощность, выделяемая топливом при горении
КПД_пгу_вд = N_пгу_вд / N_топл  # КПД ПГУ без контура низкого давления
КПД_пгу = (N_пгу_вд + N_нд) / N_топл  # КПД ПГУ с контуром низкого давления
КПД_пгу_вд, КПД_пгу, КПД_пгу - КПД_пгу_вд
Out[8]:
(0.4985731733032165, 0.5186040608962433, 0.020030887593026847)

Добавление контура низкого давления увеличило мощность ПГУ на 4%, а КПД на 2% (абсолютных).

Ссылки¶

  1. Моделирование теплообмена в котле-утилизаторе одного давления
  2. Расчёт теплофизических свойств воды и водяного пара

Инженерные расчёты на Python, С.В. Медведев, 2020-2023
Использование Python и Jupyter Notebook для инженерных расчётов, С.В. Медведев, 2020-2023