Расчёт потерь давления (напора) в отводе

Общий коэффициент гидравлического сопротивления отвода $\zeta$ для удобства инженерных расчётов в большинстве случаев определяется как сумма коэффициентов местного сопротивления $\zeta_м$ и сопротивления трения $\zeta_{тр}$ ([1]):

$$\zeta = \zeta_м + \zeta_{тр}$$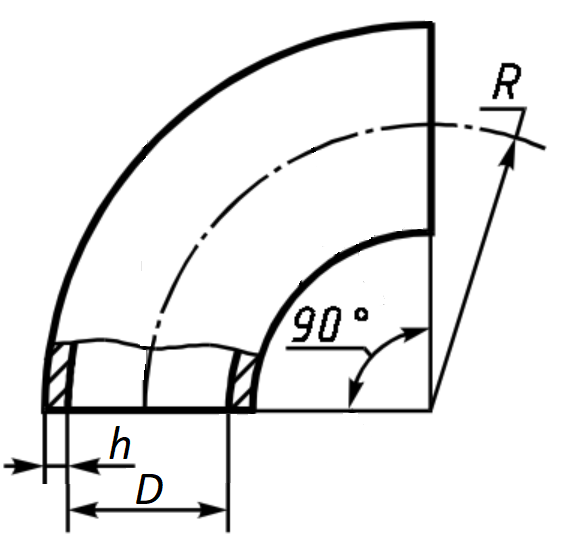

Методика и инструментарий нахождения коэффициента сопротивления трения приведены в [2]. При вычислении потерь давления от трения необходимо знать длину рассматриваемого участка. Для отвода с углом поворота $\theta$ и радиусом скругления $R$ длина пути прохождения потока внутри отвода составляет:

$$L = \frac{\pi \theta R}{180}$$

Согласно [1] коэффициент местного сопротивления отвода зависит от угла поворота отвода, его относительного радиуса закругления $R/D$, относительной шероховатости стенок отвода и режима течения (числа Рейнольдса):

$$\zeta_м = AB \cdot k_{\Delta}k_{Re},$$

где коэффициенты: $A$ учитывает угол поворота, $B$ - относительный радиус закругления, $k_{\Delta}$ - влияние относительной шероховатости на величину местных потерь, $k_{Re}$ - влияние числа Рейнольдса на величину местных потерь.

Все созданные для реализации данной расчётной методики функции включены в модуль hydrcalc (скачать версию 2). Пример использования основной расчётной функции elb_calc_dH см.здесь. Описание всех функций модуля hydrcalc касающихся расчёта гидравлического сопротивления отвода приведены здесь.

Рассмотрим влияние перечисленных выше факторов на значение коэффициента местного сопротивления.

import matplotlib as mpl
import matplotlib.pyplot as plt
plt.rcParams['font.size'] = 12
plt.rcParams['axes.grid'] = True

Угол поворота

стр. 278 в [1]

from scipy.interpolate import interp1d #интерполяция
import numpy as np #работа с массивами

degs = np.array([0, 20, 30, 45, 60, 75, 90, 110, 130, 150, 180], dtype = float)
As = np.array([0, .31, .45, .6, .78, 0.9, 1., 1.13, 1.2, 1.28, 1.4], dtype = float)
fA = interp1d(degs, As, kind='linear')
degs = np.linspace(0, 180 , 51)

fig, ax = plt.subplots()
ax.plot(degs, fA (degs))
ax.set_xlim(0, 180); ax.set_ylim(0, As[-1])
ax.set_xlabel('Угол поворота, градусы'); ax.set_ylabel('Коэффициент A');

Относительный радиус закругления $R/D$

стр. 279 в [1]

RDs = np.array([.5, .6, .7, .8, .9, 1, 1.25, 1.5, 2, 4, 6, 8, 10, 20, 30, 40])
Bs = np.array([1.18, .77, .51, .37, .28, .21, .19, .17, .15, .11, .09, .07, .07, .05, .04, .03])
fB = interp1d(RDs, Bs, kind='linear')
RD1s = np.linspace(0.5, 2. , 21)
RD2s = np.linspace(2., 40 , 51)

fig, axes = plt.subplots(1,2, figsize = (15, 5))
axes[0].plot(RD1s, fB (RD1s))
axes[0].set_xlim(0.5, 2.); axes[0].set_ylim(0,)
axes[1].plot(RD2s, fB (RD2s))
axes[1].set_xlim(2, 40); axes[1].set_ylim(0,)
for ax in axes:
    ax.set_xlabel('R/D'); ax.set_ylabel('Коэффициент B');

Число Рейнольдса

стр. 279 в [1]

#Для R/DN > 0.7
Res = np.array([.1, .14, .2, .3, .4, .6, .8, 1., 1.4, 2., 3., 4.]) * 1e5
k_Res = np.array([2, 1.89, 1.77, 1.64, 1.56, 1.46, 1.38, 1.3, 1.15, 1.02, 1., 1.])
fk_Re = interp1d(Res, k_Res, kind='linear')
Resi = np.linspace(Res[0], Res[-1], 51)
fig, ax = plt.subplots()
ax.plot(Resi, fk_Re(Resi))
formatter = mpl.ticker.ScalarFormatter(useMathText=True)
formatter.set_scientific(True)
formatter.set_powerlimits((-1,1))
ax.xaxis.set_major_formatter(formatter)
ax.set_xlim(0, Res[-1])
ax.set_xlabel('Re'); ax.set_ylabel('Коэффициент $k_{Re}$');

Из графика видно, что коэффициент $k_{Re}$ оказывает влияние на значение коэффициента местного сопротивления только при $Re<2\cdot 10^5$.

kvisc = 1e-6 #кинематичекая вязкость воды при  t = 20 C
Ds = np.linspace(20, 400, 101) * 1e-3
ws = np.linspace(0, 4, 51)
X, Y = np.meshgrid(Ds, ws)
Z = X * Y / kvisc
fig, ax = plt.subplots()
ax.set_xlabel('Внутренний диаметр трубы D, мм'); ax.set_ylabel('Скорость воды в трубе w, м/с')
ax.contourf(X*1e3, Y, Z, levels = [0, 1e5, 2e5, 2e10], colors=['red','orange', 'green'])
ax.legend(['Красная область: $Re<10^5$','Оранжевая: $10^5<Re<2\cdot 10^5$',
          'Зелёная: $Re>2\\cdot 10^5$']);

Из приведённой выше диаграммы видно, что для труб маленького диаметра и (или) при низких скоростях рабочей среды игнорирование влияния числа Рейнольдса на коэффициент местного сопротивления ведёт к занижению его значения более чем на 30% (красная зона).

Шероховатость

стр. 278 в [1]

Для гладких труб $k_{\Delta} = 1$,
Для любой шероховатости и $Re<4\cdot 10^4$ $k_{\Delta} = 1$, для $\bar{\Delta}>0.001$ и $Re > 4\cdot 10^4$ $k_{\Delta} = 2$

Для $0\le\bar{\Delta}\le 0.001$ и $Re > 2\cdot 10^5$ $k_{\Delta} = 1 + \bar{\Delta}\cdot 10^3$, при $4\cdot 10^4\le Re\le 2\cdot 10^5$ $k_{\Delta} = \lambda_{\Delta}/\lambda_{гл}$, где $\lambda_{\Delta}$ - для заданной $\Delta$, $\lambda_{гл}$ - гладкой трубы. Рассмотрим данный случай более подробно.

from hydrcalc import calc_lambda #Расчёт коэффициента сопротивления трения единицы относительной длины

#Функция для тестирования
def test_lamb(Re, delta):
    w = 3 #скорость, м/с
    kvisc = 1e-6 #кинематическая вязкость воды при t = 20 C, м2/с
    D = Re * kvisc / w #внутренний диаметр трубы, м
    Delta = delta * D #шероховатость стенок трубы, м
    return calc_lambda(w, D, Delta)

deltas = np.array([0, 1e-4, 2e-4, 4e-4, 7e-4, 1e-3])
Res = np.linspace(4e4, 2e5, 51)
ks = np.zeros((deltas.shape[0], Res.shape[0]))
for i, delta in enumerate(deltas):
    for j, Re in enumerate(Res):
        ks[i, j] = test_lamb(Re, delta) / test_lamb(Re, 0)

fig, ax = plt.subplots(figsize =(8,5))
for i, delta in enumerate(deltas):
    ax.plot(Res, ks[i][:], label = delta)
ax.set_xlim(Res[0], Res[-1])
ax.set_xlabel('$Re$'); ax.set_ylabel('$k_{\Delta}$')
ax.xaxis.set_major_formatter(formatter)
ax.legend(title = 'Относительная шероховатость $\overline{\Delta}$',ncol = 2);

Картина получается нелогичная. Видно, что для $\bar{\Delta} = 0.0001$ при $Re<0.8\cdot 10^5$ $k_{\Delta} < 1$ . Кроме того, при переходе через $Re = 2 \cdot 10^5$ значение $k_{\Delta}$ "прыгает" до значения $1 + \bar\Delta \cdot 10^3$. В связи с этим для относительных шероховатостей в диапазоне $0\le\bar{\Delta}\le 0.001$ при $Re > 4\cdot 10^4$ будем применять формулу $k_{\Delta} = 1 + \bar{\Delta}\cdot 10^3$.

Пример использования функции elb_calc_dH

from hydrcalc import elb_calc_dH

help(elb_calc_dH)

Help on function elb_calc_dH in module hydrcalc:

elb_calc_dH(Q, D, deg=90, RD=1.5, Delta=0, kvisc=1e-06, quadr=False)
    Расчёт потерь давления в отводе, метры столба жидкости
    Q: объёмный расход, м3/ч
    D: внутренний диаметр отвода, м
    deg: угол поворота, градусы (по умолчанию - 90 градусов)
    RD: относительный радиус закругления R/D (по умолчанию - R/D = 1,5)
    Delta: абсолютная шероховатость, м (по умолчанию - отсутствие шероховатости, гладкая труба)
    kvisc: кинематическая вязкость, м2/с (по умолчанию - вязкость воды при 20 С)
    quadr: False (по умолчанию) - не происходит смены формулы при Re>560/delta,
    True - при Re>560/delta применяется формула для квадратичного закона сопротивления

D_внешн = 89 #внешний диаметр трубы, мм
h = 3.5 #толщина стенки трубы, мм
deg = 45. #угол поворота
RD = 2 #относительный радиус закругления
D = D_внешн - 2 * h #внутренний диаметр, мм
D *= 1e-3 #перевод в метры
Q = 50 #объёмный расход, м3/ч
Delta=0.3e-3 #шероховатость стенок трубы, м
kvisc = 1.006e-6 #кинематическая вязкость воды при t=20 C

dH = elb_calc_dH(Q, D, deg, RD, Delta, kvisc, True)
dH

0.07990224133833408

#По умолчанию deg=90, RD=1.5, Delta=0, kvisc=1e-06, quadr=False
dH = elb_calc_dH(Q, D)
dH

0.07407393709689833

Примеры реализации расчётной методики

#Загрузим функции для расчёта гидравлического коэффициента сопротивления
#коэффициента сопротивления трения и коэффициента местного сопротивления
from hydrcalc import elb_calc_grc_w, elb_calc_frc_w, elb_calc_lrc_w

degs = np.array([30, 45, 60, 90])
w = 2 #скорость рабочей среды
RD = 1.5
Delta = 0.3e-3
kvisc = 1e-6 #кинематическая вязкость (вода при 20 С), м/с2
Ds = np.linspace(40, 1400, 501) / 1e3 #внутренние диаметры отводов, мм
grcs = np.zeros((degs.shape[0], Ds.shape[0])) #значения коэффициента гидравлического сопротивления
lrcs = np.zeros_like(grcs)
frcs = np.zeros_like(grcs)
for i, deg in enumerate(degs):
    for j, D in enumerate(Ds):
        lrcs[i,j] = elb_calc_lrc_w(w, D, deg, RD, Delta, kvisc)
        frcs[i,j] = elb_calc_frc_w(w, D, deg, RD, Delta, kvisc)
        grcs[i,j] = lrcs[i,j] + frcs[i,j]

fig, axes = plt.subplots(2, 2, figsize = (20,10))
fig.suptitle("Коэффициенты сопротивления отвода (скорость w = 2 м/с, шероховатость $\Delta = 0.3$ мм)")
for i, deg in enumerate(degs):
    axes[0][0].plot(Ds * 1e3, lrcs[i][:], label = deg)
    axes[1][0].plot(Ds * 1e3, frcs[i][:], label = deg)
    axes[1][1].plot(Ds * 1e3, grcs[i][:], label = deg)
axes[0][1].plot(Ds* 1e3, grcs[2][:], label = degs[2], color = 'green')
axes[0][0].set_xlim(0, 1400); axes[0][0].set_ylim(0.08, ); 
axes[0][1].set_xlim(40, 350); axes[0][1].set_ylim(0.26, 0.42)
axes[1][0].set_xlim(0, 1400); axes[1][0].set_ylim(0.01,)
axes[1][1].set_xlim(0, 1400); axes[1][1].set_ylim(0.1, )
axes[0][0].legend(ncol = 2, title="Угол поворота, градусы")
axes[1][0].legend(ncol = 2, title="Угол поворота, градусы")
axes[1][1].legend(ncol = 2, title="Угол поворота, градусы")
axes[0][0].set_xlabel("$D$, мм"); axes[0][0].set_ylabel("$\zeta_м$")
axes[0][1].set_xlabel("$D$, мм"); axes[0][1].set_ylabel("$\zeta_м$")
axes[1][0].set_xlabel("$D$, мм"); axes[1][0].set_ylabel("$\zeta_{тр}$")
axes[1][1].set_xlabel("$D$, мм"); axes[1][1].set_ylabel("$\zeta = \zeta_м + \zeta_{тр}$")
axes[0][0].set_title("Коэффициент местного сопротивления")
axes[0][1].set_title("Коэффициент местного сопротивления отвода $60^\circ$")
axes[1][0].set_title("Коэффициент сопротивления трения")
axes[1][1].set_title("Коэффициент гидравлического сопротивления");

Deltas = np.array([0, 0.1, 0.2, 0.3]) * 1e-3 #шероховатость стенок
deg = 90 #угол поворота
fric_rates = np.zeros((Deltas.shape[0], Ds.shape[0]))
for i, Delta in enumerate(Deltas):
    for j, D in enumerate(Ds):
        fric_rates[i,j] = elb_calc_frc_w(w, D, deg, RD, Delta, kvisc) / \
        elb_calc_grc_w(w, D, deg, RD, Delta, kvisc) * 100

fig, axes = plt.subplots(1, 2, figsize = (20,5))
fig.suptitle("Доля коэффициента сопротивления трения в коэффициенте гидравлического " +
             "сопротивления отвода $90^\circ$ (скорость w = 2 м/с)")
for i, Delta in enumerate(Deltas):
    axes[0].plot(Ds * 1e3, fric_rates[i][:], label = Delta * 1e3)
    axes[1].plot(Ds * 1e3, fric_rates[i][:], label = Delta * 1e3)
axes[0].legend(title="Шероховатость, мм"); axes[1].legend(title="Шероховатость, мм")
axes[0].set_xlim(0, 1400); axes[1].set_xlim(40, 250)
axes[0].set_xlabel("$D$, мм"); axes[0].set_ylabel("$\zeta_{тр}/\zeta$, %")
axes[1].set_xlabel("$D$, мм"); axes[1].set_ylabel("$\zeta_{тр}/\zeta$, %");

Deltas = np.array([0.1, 0.2]) *1e-3 #шероховатость стенок
grcs = np.zeros((Deltas.shape[0], degs.shape[0], Ds.shape[0]))
fig, axes = plt.subplots(1, 2, figsize = (20,5))
fig.suptitle("Коэффициент гидравлического сопротивления отвода (w = 2 м/с)")
for i, Delta in enumerate(Deltas):
    axes[i].set_title(f"$\Delta = {Delta*1e3}$ мм")  
    axes[i].set_xlabel("$D$, мм"); axes[i].set_xlim(0, 1400)
    axes[i].set_ylabel("$\zeta$");
    for j, deg in enumerate(degs):
        for k, D in enumerate(Ds):
            grcs[i,j,k] = elb_calc_grc_w(w, D, deg, RD, Delta, kvisc)
        axes[i].plot(Ds * 1e3, grcs[i][j][:], label = deg)
    axes[i].legend(ncol = 4, title="Угол поворота, градусы");

Описание функций модуля hydrcalc для расчёта потерь давления в отводе

from hydrcalc import elb_calc_dH, elb_calc_grc, elb_calc_grc_w, elb_calc_frc, \
elb_calc_frc_w, elb_calc_lrc, elb_calc_lrc_w

help(elb_calc_dH)

Help on function elb_calc_dH in module hydrcalc:

elb_calc_dH(Q, D, deg=90, RD=1.5, Delta=0, kvisc=1e-06, quadr=False)
    Расчёт потерь давления в отводе, метры столба жидкости
    Q: объёмный расход, м3/ч
    D: внутренний диаметр отвода, м
    deg: угол поворота, градусы (по умолчанию - 90 градусов)
    RD: относительный радиус закругления R/D (по умолчанию - R/D = 1,5)
    Delta: абсолютная шероховатость, м (по умолчанию - отсутствие шероховатости, гладкая труба)
    kvisc: кинематическая вязкость, м2/с (по умолчанию - вязкость воды при 20 С)
    quadr: False (по умолчанию) - не происходит смены формулы при Re>560/delta,
    True - при Re>560/delta применяется формула для квадратичного закона сопротивления

help(elb_calc_grc)

Help on function elb_calc_grc in module hydrcalc:

elb_calc_grc(Q, D, deg=90, RD=1.5, Delta=0, kvisc=1e-06, quadr=False)
    Расчёт гидравлического коэффициента сопротивления отвода (местные потери + потери трения)
    Q: объёмный расход, м3/ч
    D: внутренний диаметр отвода, м
    deg: угол поворота, градусы (по умолчанию - 90 градусов)
    RD: относительный радиус закругления R/D (по умолчанию - R/D = 1,5)
    Delta: абсолютная шероховатость, м (по умолчанию - отсутствие шероховатости, гладкая труба)
    kvisc: кинематическая вязкость, м2/с (по умолчанию - вязкость воды при 20 С)
    quadr: False (по умолчанию) - не происходит смены формулы при Re>560/delta,
    True - при Re>560/delta применяется формула для квадратичного закона сопротивления

help(elb_calc_grc_w)

Help on function elb_calc_grc_w in module hydrcalc:

elb_calc_grc_w(w, D, deg=90, RD=1.5, Delta=0, kvisc=1e-06, quadr=False)
    Расчёт гидравлического коэффициента сопротивления отвода (местные потери + потери трения)
    w: скорость потока, м/с
    D: внутренний диаметр отвода, м
    deg: угол поворота, градусы (по умолчанию - 90 градусов)
    RD: относительный радиус закругления R/D (по умолчанию - R/D = 1,5)
    Delta: абсолютная шероховатость, м (по умолчанию - отсутствие шероховатости, гладкая труба)
    kvisc: кинематическая вязкость, м2/с (по умолчанию - вязкость воды при 20 С)
    quadr: False (по умолчанию) - не происходит смены формулы при Re>560/delta,
    True - при Re>560/delta применяется формула для квадратичного закона сопротивления

help(elb_calc_frc)

Help on function elb_calc_frc in module hydrcalc:

elb_calc_frc(Q, D, deg=90, RD=1.5, Delta=0, kvisc=1e-06, quadr=False)
    Расчёт коэффициента сопротивления трения отвода
    Q: объёмный расход, м3/ч
    D: внутренний диаметр отвода, м
    deg: угол поворота, градусы (по умолчанию - 90 градусов)
    RD: относительный радиус закругления R/D (по умолчанию - R/D = 1,5)
    Delta: абсолютная шероховатость, м (по умолчанию - отсутствие шероховатости, гладкая труба)
    kvisc: кинематическая вязкость, м2/с (по умолчанию - вязкость воды при 20 С)
    quadr: False (по умолчанию) - не происходит смены формулы при Re>560/delta,
    True - при Re>560/delta применяется формула для квадратичного закона сопротивления

help(elb_calc_frc_w)

Help on function elb_calc_frc_w in module hydrcalc:

elb_calc_frc_w(w, D, deg=90, RD=1.5, Delta=0, kvisc=1e-06, quadr=False)
    Расчёт коэффициента сопротивления трения отвода
    w: скорость потока, м/с
    D: внутренний диаметр отвода, м
    deg: угол поворота, градусы (по умолчанию - 90 градусов)
    RD: относительный радиус закругления R/D (по умолчанию - R/D = 1,5)
    Delta: абсолютная шероховатость, м (по умолчанию - отсутствие шероховатости, гладкая труба)
    kvisc: кинематическая вязкость, м2/с (по умолчанию - вязкость воды при 20 С)
    quadr: False (по умолчанию) - не происходит смены формулы при Re>560/delta,
    True - при Re>560/delta применяется формула для квадратичного закона сопротивления

help(elb_calc_lrc)

Help on function elb_calc_lrc in module hydrcalc:

elb_calc_lrc(Q, D, deg, RD, Delta, kvisc)
    Расчёт коэффициента местного сопротивления отвода
    Q: объёмный расход, м3/ч
    D: внутренний диаметр отвода, м
    deg: угол поворота, градусы (по умолчанию - 90 градусов)
    RD: относительный радиус закругления R/D (по умолчанию - R/D = 1,5)
    Delta: абсолютная шероховатость, м (по умолчанию - отсутствие шероховатости, гладкая труба)
    kvisc: кинематическая вязкость, м2/с (по умолчанию - вязкость воды при 20 С)
    quadr: False (по умолчанию) - не происходит смены формулы при Re>560/delta,
    True - при Re>560/delta применяется формула для квадратичного закона сопротивления

help(elb_calc_lrc_w)

Help on function elb_calc_lrc_w in module hydrcalc:

elb_calc_lrc_w(w, D, deg, RD, Delta, kvisc)
    Расчёт коэффициента местного сопротивления отвода
    w: скорость потока, м/с
    D: внутренний диаметр отвода, м
    deg: угол поворота, градусы (по умолчанию - 90 градусов)
    RD: относительный радиус закругления R/D (по умолчанию - R/D = 1,5)
    Delta: абсолютная шероховатость, м (по умолчанию - отсутствие шероховатости, гладкая труба)
    kvisc: кинематическая вязкость, м2/с (по умолчанию - вязкость воды при 20 С)
    quadr: False (по умолчанию) - не происходит смены формулы при Re>560/delta,
    True - при Re>560/delta применяется формула для квадратичного закона сопротивления

Ссылки

1. И.Е. Идельчик. Справочник по гидравлическим сопротивлениям. 3-е издание переработанное и дополненное. Москва. "Машиностроение". 1992 г.
2. Расчёт потерь давления (напора) в трубе

Инженерные расчёты на Python, С.В. Медведев, 2020
Использование Python и Jupyter Notebook для инженерных расчётов, С.В. Медведев, 2020