Подбор регулирующего клапана

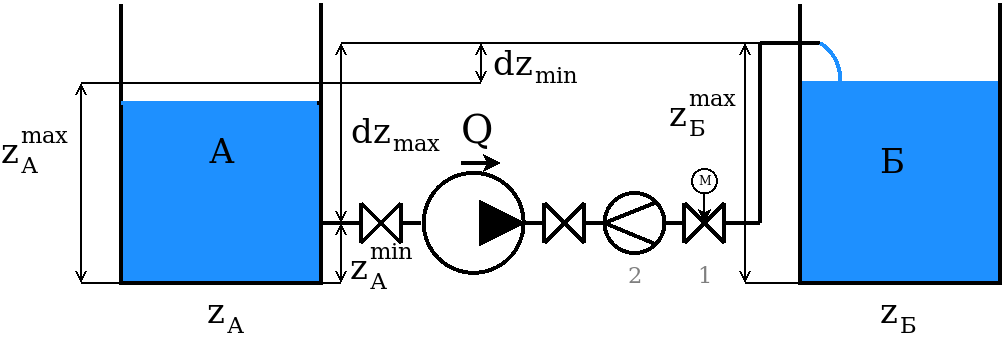
Изменим условия задачи из [1]. Насос работает постоянно, его подача должна регулироваться в диапазоне [$Q_{min}; Q_{max}$]. Регулирование расхода может осуществляться либо с помощью частотно-регулируемого привода (ЧРП) либо установкой в линии регулирующего клапана (РК). Рассмотрим вариант с РК (1 на рисунке). Величина расхода измеряется расходомером (2 на рисунке). Примем, что расходомер имеет нулевое гидравлическое сопротивление.

Расчётная схема

В [2] приведены расходные характеристики регулирующих клапанов с диапазоном регулирования $Д=50$ (относительная начальная пропускная способность РК $\Phi_0 = 1/50=0.02$) и различными типами пропускных характеристик.

Выберем РК с равнопроцентной пропускной характеристикой (третий график в [2]) со значением авторитета 0,1. При выборе величины авторитета РК следует иметь в виду, что чем больше значение авторитета РК тем с большей величиной напора потребуется насос для решения поставленной задачи. Насос с большим напором будет потреблять больше электроэнергии в течение всего срока службы системы. При маленьком значении авторитета РК имеет низкую чувствительность в области положения штока около h=1. Подробнее см. в [2].

Из [1] возьмём данные о гидравлическом сопротивлении соединяющего два бака трубопровода.

В Таблице 1 в [4] ближайшим большим к полученному расчётному значению $K_{Vs}$ является $K_{Vs}=100$ $м^3/ч$.

При решении практических задач следует помнить, что существует производственный допуск на значение $K_{Vs}$ РК. В [6] сказано, что для РК с равнопроцентной пропускной характеристикой отклонение от номинального значения условной пропускной способности не должно превышать $\pm 15 \%$.

В контексте нашего случая это означает, что фактическое значение условной (максимальной) пропускной способности РК с номинальным $K_{Vs}=100\ м^3/ч$ может лежать в диапазоне

С течением времени характеристики насоса ухудшаются, его подача уменьшается при неизменном гидравлическом сопротивлении сети - происходит деградация напорной характеристики насоса. Графически деградация напорной характеристики насоса выражается в смещении напорной характеристики насоса вниз. Т. к. расход $Q_{max}$ должен обеспечиваться в течение всего срока службы насоса, то насос должен быть выбран таким образом, чтобы он и в изношенном состоянии обеспечивал подачу $Q_{max}$.

Таким образом РК и насос должны быть подобраны таким образом, чтобы удовлетворялись следующие условия:

  1. При полностью открытом РК_н при условии старых труб, изношенном насосе и минимальном уровне в баке А расход составляет не менее $Q_{max}$,
  2. При условии новых труб, максимальном уровне в баке А, новом насосе и расходе не более $Q_{min}$ в РК отсутствует кавитация (при положении штока $h=h_{min}$, где $h_{min}$ - минимальное для всех возможных состояний и режимов работы сети положение штока, при котором расход не превышает $Q_{min}$).

Необходимо создать модели напорных характеристик для нового и изношенного насоса. Через рабочую точку [Q_max; H_Q_max] должна проходить напорная характеристика изношенного насоса.

Примем величину деградации напорной характеристики насоса за весь срок службы 10%.

При любом режиме работы и состоянии сети расход в диапазоне [35; 55] $м^3/ч$ будет обеспечивается положением штока РК в диапазоне [h_min; 1].

Следует заметить, что в левой граничной точке перепад давления на РК будет один и тот же вне зависимости от фактического значения $K_{Vs}$ РК. Это достигается разными положениями штоков у РК_н и РК_в.

Проверка на кавитацию

Самый опасный с точки зрения возможности возникновения кавитации режим работы РК - это режим работы при котором на РК возникает наибольший перепад давления. Данный режим возникает при условии нового насоса, новых труб, максимальном уровне в баке А и положении штока РК $h=h_{min}$ (левая граничная точка на рисунке выше).

У РК с одноступенчатой редукцией кавитация отсутствует если выполнено следующее условие: $$K = \frac{p_1-p_2}{p_1 - p_{нас}} = \frac{\Delta p_{рк}}{p_1 - p_{нас}} \le 0.6$$ $p_1$ - давление перед РК, $p_2$ - давление за РК, $p_{нас}$ - давление насыщенного пара при температуре перекачиваемой воды, $\Delta p_{рк}$ перепад давления на РК. Чем выше значение $p_1$ при неизменном $\Delta p_{рк}$ тем меньше значение коэфициента $K$, а значит, тем лучше условия для обеспечения безкавитационной работы.

Давление перед РК зависит среди прочего от места установки РК. $$p_1 = p_{вс} + H - \Delta p + \Delta z$$ $p_{вс}$ - давление на всасе насоса, $H$ - напор насоса, $\Delta p$ - потери давления в линии от бака А до РК, $\Delta z$ - нивелирная составляющая (разница между высотным положением входного патрубка насоса и высотным положением РК).

Рассмотрим самый неблагоприятный с точки зрения отсутствия кавитации случай: когда РК расположен в самой высокой точке сети - на высоте $z_Б^{max}$ (см. рисунок в начале статьи) в непосредственной близости к баку Б.

Из [1] возьмём данные о высотных положениях элементов сети.

При $t=20$ C $p_{нас}=2339.2$ Па (см. [5])

$K > 0.6$ означает, что при условии новых труб, нового насоса и высокого уровня в баке А при прикрытии одноступенчатого РК, с целью снижения расхода перекачиваемой воды до $Q_{min}$, возникает кавитация.
Выходом из данной ситуации может являться:

  1. применение РК с многоступенчатой редукцией у которого коэффициент начала кавитации должен быть $K_c \ge 0.82$;
  2. использование РК, конструкция (материал) которого предусматривает его длительную работу в режиме кавитации;
  3. изменение места установки РК.

Посмотрим, что изменится если установить РК сразу за насосом. Для упрощения примем, что потери в трубопроводе происходят за РК и потери давления на участке между баком А и РК отсутствуют.

$K < 0.6$, значит при любых режимах работы и состоянии системы РК сможет в бескавитационном режиме работы обеспечить регулирование расхода в диапазоне [$Q_{min}; Q_{max}$].

Расходные характеристики

Построим две расходные характеристики:

  1. РК_н при условии старых труб, изношенном насосе и минимальном уровне в баке А
  2. РК_в при условии новых труб, новом насосе и максимальном уровне в баке А

Для первого случая ранее был определён расход и напор насоса при полностью открытом РК_н: Q_max и H_Q_max соответственно.

Найдём точку пересечения характеристики трубопровода с напорной характеристикой нового насоса

Разница между ранее найденным значением h_min и значением h_min из расходной характеристики объясняется тем, что при построении расходной характеристики не учитывавается увеличение напора насоса при уменьшении его подачи. Влияние наклона напорной характеристики насоса на форму расходной характеристики РК рассмотрено в [8].

Ссылки

  1. Подбор насоса
  2. Расходная характеристика регулирующего клапана
  3. Расчёт параметров регулирующего клапана
  4. ГОСТ 23866-87 Клапаны регулирующие односедельные, двухседельные и клеточные. Основные параметры
  5. Зависимость давления насыщения водяного пара от температуры
  6. ГОСТ 12893-2005 Клапаны регулирующие односедельные, двухседельные и клеточные. Общие технические условия
  7. Моделирование характеристики гидравлической сети
  8. Зависимость формы расходной характеристики регулирующего клапана от наклона напорной характеристики насоса

Инженерные расчёты на Python, С.В. Медведев, 2020-2021
Использование Python и Jupyter Notebook для инженерных расчётов, С.В. Медведев, 2020-2021