Моделирование разделительного трёхходового регулирующего клапана

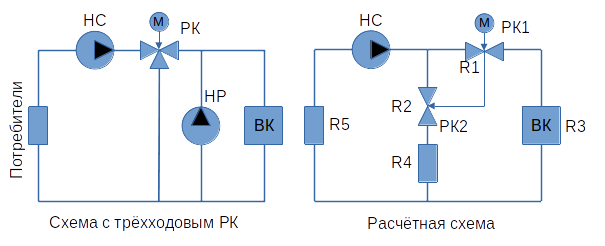
Рассмотрим систему, состоящую из сетевого насоса (НC), рециркуляционного насоса (НР), водогрейного котла (ВК), трёхходового разделительного регулирующего клапана (РК) и потребителей тепловой энергии.

Рециркуляционный насос предназначен для поддержания температуры воды на входе в котёл не ниже предельного значения, которое зависит от температуры точки росы продуктов сгорания топлива.

Разделительный трёхходовой регулирующий клапан устанавливается для получения возможности подмеса холодной обратной сетевой воды (до ВК) в трубопровод горячей прямой сетевой воды (после ВК) с целью снижения температуры прямой сетевой воды. РК включается в работу в ситуации когда невозможно с помощью уменьшения подачи топлива в котёл снизить температуру воды на выходе из ВК до требуемого значения.

На правом рисунке приведена расчётная схема, в которой трёхходовой регулирующий клапан представлен двумя двухходовыми.

R - гидравлическое сопротивление участка трубопровода (более подробно см. [1]).

В нормальном режиме работы РК открыт (относительное положение штока $\bar h = 1$). В расчётной схеме открытому РК соответствуют открытый РК1 ($\bar h_1 = 1$) и закрытый РК2 ($\bar h_2 = 0$). При открытии РК2 на $\Delta \bar h$ РК1 закрывается на ту же величину $\Delta \bar h$.

Q = 300  # номинальный расход через водогрейный котёл, м3/ч
H = 8e5  # напор насоса, Па
Kvs = 800. # условная пропускная способность РК, м3/ч
F0 = 1/50  # регулировочное отношение

dp3 = 50e3 # падение давления в ветке ВК (без учёта РК1) при расходе Q, Па
dp4 = 10e3 # падение давления в ветке РК2 (без учёта РК2) при расходе Q, Па
R3 = dp3/Q/Q; R4 = dp4/Q/Q  # гидравлические сопротивления (см. [1])

В нормальном режиме работы РК1 полностью открыт, а РК2 закрыт. Найдём значение R5 при котором при заданном значении напора сетевого насоса $H$ суммарный расход в линии потребителей будет составлять $Q$.

$H = (R_1 + R_3 + R_5)Q^2$ отсюда $R_5 = H/Q^2 - R_1 - R_3$

Требуемое значение R5 достигается посредством установки в линиях потребителей балансировочных шайб или регулирующих клапанов (см. [3]).

Построим зависимости расходов и перепадов давлений в каждой ветке (РК1, РК2) от положения штока РК для различных комбинаций видов пропускных характеристик РК1 и РК2.

# Создаём объект класса ControlValve.
# ControlValve - модель регулирующего клапана (см. [2])
from controlvalve import ControlValve
cv1 = ControlValve(Kvs, 0, F0)
R1 = cv1.get_R()  # гидравлическое сопротивление открытого РК
R5 = H / Q / Q - R1 - R3

from scipy import optimize
import numpy as np

def f(xs):
    #функция для optimize.root, возвращает нули если xs - решения уравнений
    #xs - значения расходов через РК1 и РК2
    dp = H - R5 * (xs[0] + xs[1]) ** 2  # перепад давления на ветках РК1 и РК2
    dp1 = xs[0] * xs[0] * (R1 + R3)  # потери давления в контуре РК1
    dp2 = xs[1] * xs[1] * (R2 + R4)  # потери давления в контуре РК2
    return [dp - dp1, dp - dp2]

chars = ['линейная', 'равнопроцентная']
hs = np.linspace(0, 1, 51)
Qs = np.zeros((len(hs), 3))
dps = np.zeros((len(chars), len(chars), len(hs), 2))
xs_0 = [Q/2, Q/2]

import matplotlib.pyplot as plt
plt.rcParams['font.size'] = 18
fig, axes = plt.subplots(len(chars),len(chars), figsize = (25, 15))
for j in range(len(chars)):
    # Создаём объект класса ControlValve (см. [1])
    cv1 = ControlValve(Kvs, j, F0)
    for k in range(len(chars)):
        cv2 = ControlValve(Kvs, k, F0)
        for i, h in enumerate(hs):
            cv1.set_h(h)
            R1 = cv1.get_R()
            cv2.set_h(1 - h)
            R2 = cv2.get_R()
            sol = optimize.root(f, xs_0)
            Qs[i, 0] = sol.x[0]; Qs[i, 1] = sol.x[1]
            Qs[i, 2] = sol.x[0] + sol.x[1]
            dps[j, k, i, 0] = cv1.dp_from_Q(sol.x[0])
            dps[j, k, i, 1] = cv2.dp_from_Q(sol.x[1])
        axes[j][k].plot(hs, Qs)
        axes[j][k].set_title('РК1 '+ chars[j] + ', РК2 ' + chars[k])
        axes[j][k].grid();  axes[j][k].set_xlim(0,1);  axes[j][k].set_ylim(0,350)
        axes[j][k].legend(['$Q_1$', '$Q_2$', '$Q$']);
        axes[j][k].set_xlabel('$\overline{h}$'); axes[j][k].set_ylabel('$Q,\ м^3/ч$')

fig, axes = plt.subplots(len(chars),len(chars), figsize = (25, 15))
for j in range(len(chars)):
    for k in range(len(chars)):
        axes[j][k].plot(hs, dps[j,k] / 1e5)
        axes[j][k].set_title('РК1 '+ chars[j] + ', РК2 ' + chars[k])
        axes[j][k].grid();  axes[j][k].set_xlim(0,1)
        axes[j][k].legend(['$\Delta p_1$', '$\Delta p_2$']);
        axes[j][k].set_xlabel('$\overline{h}$'); axes[j][k].set_ylabel('$\Delta p,\ бар$')

Ссылки

1. Моделирование характеристики гидравлической сети
2. Расчёт параметров регулирующего клапана
3. Гидравлическая балансировка сети
4. Моделирование смесительного трёхходового регулирующего клапана

Инженерные расчёты на Python, С.В. Медведев, 2020-2022
Использование Python и Jupyter Notebook для инженерных расчётов, С.В. Медведев, 2020-2022