Зависимость КПД гидравлической системы от расхода при регулировании расхода дросселированием¶
Рассмотрим систему теплоснабжения, в которой расход теплоносителя регулируется дросселированием с помощью регулирующего клапана (далее - РК).
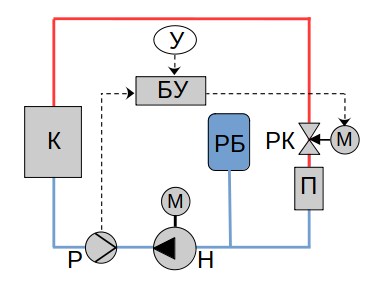
Рассмотрим систему теплоснабжения, в которой расход теплоносителя регулируется дросселированием с помощью регулирующего клапана (далее - РК).

В качестве рассматриваемого насоса возьмём Grundfos CR 3-3 (см. [1]).
# Моделирование характеристик насоса Grundfos CR 3-3
import numpy as np # работа с массивами
from scipy.interpolate import interp1d # интерполяция/экстраполяция
# Напорная характеристика насоса
# Возьмём несколько точек с напорной характеристики (включая две крайних)
Qs = np.array([1.19, 2, 3, 4, 4.43])
Hs = np.array([18.01, 16.55, 13.64, 8.91, 6.14])
f_head = interp1d(Qs, Hs, kind = 'cubic') # интерполирующая функция для напора
# КПД насоса при расходе Qs
effs = [0.13, 0.19, 0.23, 0.21, 0.184]
f_eff = interp1d(Qs, effs, kind = 'cubic') # интерполирующая функция для КПД
# Набор значений Q и H для построения графиков
Q_макс = Qs[-1]; Q_мин = Qs[0]
Q1s = np.linspace(Q_мин, Q_макс)
H1s = np.array(list(map(f_head, Q1s)))
# Границы рабочего диапазона насоса
Q_мин, Q_макс # м3/ч
(1.19, 4.43)
import matplotlib.pyplot as plt
plt.rcParams['font.size'] = 12.0
fig, ax = plt.subplots(figsize = (10, 5))
ax.set_xlabel('$Q,\,м^3/ч$');
ax.set_ylabel('$H,\,м$')
ax.plot(Q1s, H1s, label = 'Напор, м');
ax.grid()
ax.set_title("Характеристики насосного агрегата (насос + электродвигатель)")
ax.set_xlim(1., 4.5); ax.set_ylim(6, 20);
ax2 = ax.twinx();
ax2.plot(Q1s, np.array(list(map(f_eff, Q1s))) * 100, label = 'КПД, %', color = 'red');
ax2.set_ylim(12, 26);
ax2.set_ylabel('$\eta,\ \%$');
# Объединение легенд двух графиков в одну общую
h1, l1 = ax.get_legend_handles_labels()
h2, l2 = ax2.get_legend_handles_labels()
ax.legend(h1+h2, l1+l2, loc=6);
Зададим авторитет РК равным 10% (доля напора насоса, затрачиваемая на преодоление сопротивления полностью открытого РК при расходе $Q_{макс}$). Оставшиеся 90% напора затрачивается на преодоление сопротивлений потребителя, котла и расходомера.
# При Q_макс
dp_рк = 0.1 * Hs[-1] # Перепад давления на РК, 0.1 (10%) - авторитет РК
Определим что происходит при изменении расхода в системе с $Q_{макс}$ до $Q_{мин}$ посредством прикрытия РК.
КПД гидравлической системы для заданного значения подачи (расхода) $Q$ находится по формуле:
$$\eta_с = \eta_н \frac{H_{тр}}{H_н}$$где, $\eta_с$ - КПД системы, $\eta_н$ - КПД насосного агрегата (насос + электродвигатель) для заданного $Q$, $H_{тр}$ - требуемый напор для заданного $Q$, $H_н$ - напор насоса для заданного $Q$.
Электрическая мощность, затрачиваемая на преодоление сопротивления РК:
$$P_{пот} = (H_н-H_{тр})\rho gq / \eta_н$$где $P_{пот}$ - потери электрической мощности, Вт; $\rho$ - плотность перекачиваемой жидкости, кг/м3; $g$ = 9,81 м/с2 - ускорение свободного падения; $H_н$ - напор насоса, м; $H_{тр}$ - требуемый напор, м; $q=Q/3600$ - подача насоса, м3/с; $Q$ - подача насоса, м3/ч; $\eta_н$ - КПД насосного агрегата.
# Сопротивление гидравлической сети без РК
R_без_рк = (Hs[-1] - dp_рк) / Q_макс / Q_макс
# Требуемый напор
Hs_треб = [R_без_рк * Q * Q for Q in Q1s]
# КПД гидравлической системы
effs_сист = np.array([f_eff(Q) for Q in Q1s]) * Hs_треб / H1s
plt.rcParams['font.size'] = 12.0
fig, ax = plt.subplots(figsize = (10, 5))
ax.set_xlabel('$Q,\,м^3/ч$');
ax.set_ylabel('$H,\,м$')
ax.plot(Q1s, H1s, label = 'Напор насоса, м');
ax.plot(Q1s, Hs_треб, label = 'Требуемый напор, м');
ax.grid()
ax.set_title("Характеристики насосного агрегата и гидравлической системы")
ax.set_xlim(1., 4.5); ax.set_ylim(0, 20);
ax2 = ax.twinx();
ax2.plot(Q1s, np.array(list(map(f_eff, Q1s))) * 100, label = 'КПД насоса, %', color = 'red');
ax2.plot(Q1s, effs_сист * 100, label = 'КПД системы, %', color = 'green');
ax2.set_ylim(0, 24); ax2.yaxis.set_ticks(np.arange(0, 25, 3))
ax2.set_ylabel('$\eta,\ \%$');
# Объединение легенд двух графиков в одну общую
h1, l1 = ax.get_legend_handles_labels()
h2, l2 = ax2.get_legend_handles_labels()
ax.legend(h1+h2, l1+l2, loc=6);
# Влияние авторитета РК на КПД системы и напор насоса
effs_сист[-1] / f_eff(Qs[-1]), Hs_треб[-1] / Hs[-1]
(0.9000000000000001, 0.9000000000000001)
"Требуемый напор" - это напор, которого достаточно, чтобы обеспечить нужный расход в системе без РК. Так же "Требуемый напор" является характеристикой гидравлической сети без РК (см. [2]).
Разница в значениях напора насоса и требуемого напора при подаче $Q_{макс}$ равна перепаду давления на полностью открытом РК (в нашем случае 10% от значения напора при подаче $Q_{макс}$, т.к. мы приняли авторитет РК равным 10%). Так же при подаче $Q_{макс}$ КПД системы меньше КПД насоса на те же 10% (относительных).
Чем выше значение авторитета РК тем ниже максимальный КПД системы при прочих равных условиях.
Расход уменьшается путём прикрытия РК. Чем больше прикрывается РК тем больше на нём становится перепад давления, а значит, тем большая часть напора насоса расходуется бесполезно.
Чем круче напорная характеристика насоса тем на большую величину снижается КПД системы при уменьшении расхода. Это объясняется тем, что при снижении расхода требуемый напор так же уменьшается, а напор насоса увеличивается, и чем в большей степени напор насоса увеличивается тем большую часть этого напора приходится дросселировать (терять).
Если насос должен работать в широком диапазоне подач, то в этом случае лучше использовать насос с частотно-регулируемым приводом (см. [3]).
Инженерные расчёты на Python, С.В. Медведев, 2020-2022
Использование Python и Jupyter Notebook для инженерных расчётов, С.В. Медведев, 2020-2022