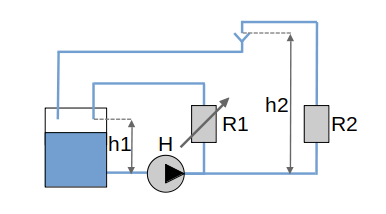
 Рассмотрим следующую схему. Имеется насос объёмного типа Н, предназначенный для подачи масла из маслобака на подшипники турбины, на выходе из которых масло самотёком возвращается в маслобак.
Рассмотрим следующую схему. Имеется насос объёмного типа Н, предназначенный для подачи масла из маслобака на подшипники турбины, на выходе из которых масло самотёком возвращается в маслобак.
$R_1$ - регулирующий клапан с переменным гидравлическим сопротивлением, $R_2$ - сопротивление трубопровода от напора насоса до выходного сечения маслопровода, подводящего масло к подшипнику, $h_1$ - отметка выходного сечения линии рециркуляции, $h_2$ - отметка выходного сечения подающего маслопровода.
Рассматриваемое масло - масло Тп-22.
Теплофизические свойства масла Тп-22 https://openedu.urfu.ru/files/book/_static/pages/2.8.html